
Тригонометричні функції

by Tetyana Masych
Artwork: Тетяна Масич
- Joined Jun 2023
- Published Books 20
Copyright © 2023

Зміст
1.Теоретичні відомості…………………………………………3 – 14
2.Приклади розв’язування типових завдань………15 – 20
3.Тести……………………………………………………………………21 – 22
4.Підготовка до НМТ з математики………………………23 – 24
5.Відео……………………………………………………………………25 – 27
6.Завдання для самостійної роботи……………………..28

Теоретичні відомості
Познайомимося з поняттями синуса, косинуса, тангенса і котангенса будь – якого кута за допомогою одиничного кола.
Означення: Коло з центром у початку координат і радіусом, що дорівнює 1, називається одиничним колом.

Означення: Синусом кута називають ординату точки одиничного кола, яка відповідає даному куту.
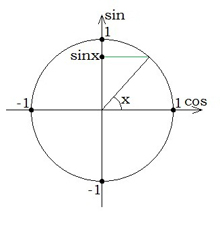
Означення: Косинусом кута називають абсцису точки одиничного кола, яка відповідає даному куту.
Означення: Тангенсом кута називають відношення синуса даного кута до його косинуса.
Означення: Котангенсом кута називають відношення косинуса даного кута до його синуса.
Синус, косинус, тангенс і котангенс разом називають тригонометричними функціями.
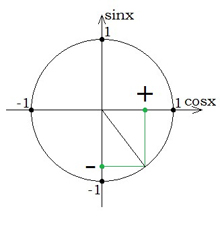
Знаки тригонометричних функцій

Кути вимірюють у градусах та радіанах.
Градусна і радіанна міри кутів пов’язані такими залежностями:
Точні значення тригонометричних функцій при деяких значеннях аргументу наведені в таблиці:


Основні співвідношення між тригонометричними функціями одного аргументу
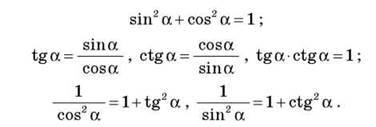

Формули зведення
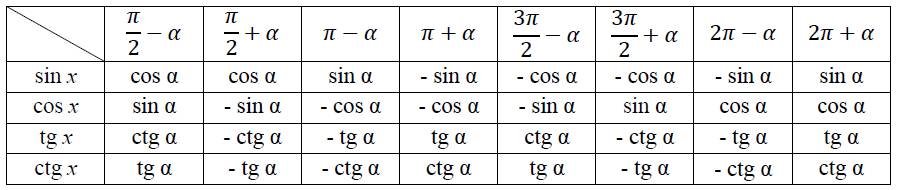
Правило зведення
Якщо кут даної тригонометричної функції відкладається від вертикального діаметра, то її замінюють кофункцією, якщо ж – від горизонтального діаметра, то її назву не змінюють.
Знак ставлять такий, який має значення даної функції за умови, що кут гострий.
![]()
Властивості та графіки тригонометричних функцій
1. y = sinx

2. y = cosx

3. у = tg х

4. у = ctg х

Періодичність тригонометричних функцій
Означення: Функція називається періодичною з періодом Т ≠ 0, якщо для будь-якого х з області визначення функції числа х + Т та х – Т також належать області визначення і виконується умова: f (х) = f (х + Т) = f (х – Т).
Найменшим додатним періодом функцій sinx і cosx
є число 2π.
Для функцій tg х і ctg х найменший додатний період π.
Формула для знаходження найменшого додатного періода функції у = А · f (kx + m) + B
Т =Т1 / lkl
Парність та непарність тригонометричних функцій
Означення: Функція називається парною, якщо для будь – якого х з області визначення виконується рівність:
f(-х) = f(х).
Означення: Функція називається непарною, якщо для будь – якого х з області визначення виконується рівність:
f(-х) = – f(х).
Синус, тангенс і котангенс є непарними функціями.
Косинус – функція парна.

Приклади розв’язування типових завдань
Задача 1: Запишіть у радіанній мірі кути:
Задача 2: Запишіть у градусах кут, радіанна міра якого дорівнює:
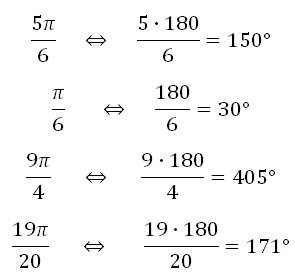
Задача 3: Позначте на одиночному колі точки, які відповідають числам:
а) π/6 + 2πn , π/4 + 2πn, π/3 + 2πn, π/2 + 2πn, 2π/3 + 2πn, 3π/4 + 2πn , 5π/6 + 2πn, 7π/6 + 2πn, 5π/4 + 2πn, 4π/3 + 2πn, 5π/3 + 2πn, 7π/4 + 2πn, 11π/6 + 2πn, де n є Ζ.
Підказка: використайте матеріал із задачі 2.

Задача 4: Обчисліть: а) sin π + sin 1,5π;
б) cos0 + cos 3,5π – cos 3π.
Розв’язання:
а) sin π + sin 1,5π = 0 + ( -1) = -1;
б) cos0 + cos 3,5π – cos 3π = 1 + 0 – (-1) = 1 + 1 = 2
Задача 5: Визначте знак числа: а) tg 3π/4 ; б) tg (- 5π/6) ; в) ctg ( – π/3).
Розв’язання:
а) tg 3π/4 = 3 · 180°/4 = 135° – знак мінус(2 чверть);
б) tg (- 5π/6) = -5 · 180°/6 = -150° – знак плюс(2 чверть, мінус на мінус = плюс);
в) ctg ( – π/3) = -180°/6 = -30° – знак мінус(1 чверть).

Задача 6: Спростіть вираз: ctg(-х) · tg(-х) – sin2 х
Розв’язання:
ctg(-х) · tg(-х) – sin2 х = – ctg х · (-tg х) – sin2 х = 1 – sin2 х = cos2х.
Ми використали тригонометричну формулу, а також дослідили функції тангенса і котангенса на парність (непарність).
Задача 7: Спростіть вираз:

Ми використали формули зведення.

Задача 8: Знайдіть період функції: у = 3 sin(2х + π/6).
Розв’язання:
Формула Т =Т1 / lkl = 2π/2 = π.
Відповідь: Період функції дорівнює π.
Задача 9: Дослідити на парність функцію f(x)=3x-tgx.
Розв’язання:
f(-х) = 3 · (-х) – tg(-x) = -3х + tgx = – (3x-tgx) = –f(х).
Відповідь: дана функція є непарною.


2. Виконайте інтерактивну вправу:

Підготовка до НМТ з математики
Виконайте завдання за посиланням:
https://zno.osvita.ua/mathematics/tag-pokaznykovi_logharyfmichni_tryghonometrychni_funkciyi/
Важливо!
Виконуйте тільки ті завдання, які стосуються теми: “Тригонометричні функції”
![]()
Відео
Перегляньте навчальні відео:
Завдання для самостійної роботи
1.Чому дорівнює радіанна міра кута 180° ?
2. Переведіть градусну міру кута 135° в радіанну.
3. Чому дорівнює градусна міра кута π/2?
4. Переведіть радіанну міру кута π/3 в градусну.
5.Спростіть вираз: 1 – сos2х.
6. Спростіть вираз: (1 – sin2 х) · tg2х.
7. Для функції у = tg х знайти у(π/3).
8. Який знак має вираз sin112° ?
9. Який знак має вираз сos 221° ?
10.Яке з тверджень про функцію є неправильним ?
а) множина значень функції Е(у) = [-1;1]
б) функція непарна;
в) функція зростає на проміжку (-∞;+∞) .

Published: Jun 23, 2023
Latest Revision: Jun 23, 2023
Ourboox Unique Identifier: OB-1471263
Copyright © 2023








