Рекурсията е явление в програмирането, при което едно понятие се дефинира чрез самото себе си.
Тя дава възможност за крайна дефиниция на безкрайно множество. Посредством рекурсия се описват много математически структури и формули, като тяхното моделиране и обработка става удобно чрез рекурсивни методи.

Рекурсията условно се разделя в две категории: директна (пряка) и индиректна (косвена).
Директна рекурсия – в дефиницията на функцията се съдържа непосредствено обръщение към самата функция.
Индиректна рекурсия – функцията funcR извиква функцията funcD, която от своя страна вика отново функцията funcR.
int funcR(int p){
…
a= b+funcR(c);
…
}
int funcR(int p){
…
a= b+funcD(c);
…
}
int funcD(int p){
…
if(a>2)d= b+funcR(m);
…
}

Обяснение на рекурсията
Рекурсията в програмирането обикновено се обяснява с практически реализации в съответния език за програмиране. Ако се излезе и извън рамките на използвания синтаксис, концептуално рекурсията може да бъде оприличена на играчката матрьошка. Началото на рекурсията се оприличава с първоначалното състояние на играчката – една голяма кукла. При отваряне, вътре се намира по-малка версия на куклата, после още по-малка версия и така n на брой пъти, докато се стигне до т.нар. дъно на рекурсията, представляващо най-малкото копие на същата кукла, която не може да бъде отворена или манипулирана по някакъв начин. Когато се използва рекурсия трябва да се вземе предвид кога ще бъде достигнато дъното ѝ.


Дъглас Хофстетър
Дъглас Хофстетър обяснява в пета глава на книгата си „An Eternal Golden Braid“ принципа на стека чрез служител на компания: той разговаря по своя телефон с потребител А, когато друг потребител Б се обажда в същия момент. Служителят слага А на изчакване и се фокусира върху Б, докато не получава трето обаждане от потребител В. Потребител Б е оставен на изчакване, докато не приключи разговора с потребител В. После служителят се връща към Б, докато не се появи четвърти потребител Г. След приключване на последния разговор служителят може да се върне към потребител Б и впоследствие към А. Тази базова аналогия от ежедневието демонстрира рекурсивно поведение в стек, където всеки следващ елемент бива добавен и респективно изваждан от стека. Това са понятията „push“ и „pop“. „Push“ обозначава спирането на конкретната операция, запомнянето на състоянието ѝ и поемането на нова задача, която стои на по-ниско ниво. „Pop“ извършва обратния процес, а именно затварянето на операцията на по-ниско ниво и връщането към предходната, която е с едно ниво нагоре.
Видове рекурсия
Единична и множествена рекурсия
Рекурсия, която съдържа само едно извикване се нарича единична рекурсия, а рекурсия, при която е налице многократно извикване се нарича множествена рекурсия. Стандартни примери за единична рекурсия са:
-обхождане на списък
-линейно търсене
-изчисляване на факториел
За естествено число n да се изчисли n! = 1 * 2 * 3 * … * n. Например, ако n = 5, то резултатът ще
бъде: 5! = 1 * 2 * 3 * 4 * 5 = 120.
а такива за множествена рекурсия са:
-обхождане на дърво
-обхождане в дълбочина
-намиране членовете на редица на Фибоначи.

Косвена рекурсия
Най-разпространените примери за рекурсия демонстрират пряка рекурсия, при която извикването е директно. За да е налице случай на косвена рекурсия е необходимо извикване от друга функция. Например, ако при прилагането на рекурсивен подход f извиква f, се касае за случай на пряка рекурсия, но ако f извиква g, който от своя страна вика f, тогава има налице косвена рекурсия на f. Срещат се и случаи на верижни (три или повече) функционални извиквания; например, функция 1 извиква функция 2, функция 2 извиква функция 3, и функция 3 извиква отново функция 1.
Пряка рекурсия
int foo(int x)
{
if (x <= 0) return x;
return foo(x – 1);
}
Косвена рекурсия
int foo(int x)
{
if (x <= 0) return x;
return foo1(x);
}
int foo1(int y)
{
return foo(y – 1);
}
Анонимна рекурсия
Анонимната рекурсия е рекурсия, която не вика функцията по име, а по-скоро имплицитно я призовава в зависимост от текущия контекст. Това се реализира в някои програмни езици чрез ключове (или други конструкции), които позволяват референция.
Акумулираща рекурсия
int foo (int n)
{
if (n == 0) return 1;
return n * foo(n – 1);
}
Споделена рекурсия
int foo(int x)
{
if (x <= 0) return x;
return foo1(x);
}
int foo1(int y) {
return foo(y – 1);
}
Нелинейна рекурсия
int foo(int n)
{
if (n == 0) return 0;
if (n == 1) return 1;
return foo(n – 1) + foo(n – 2);
}
Структурна и генеративна рекурсия
Някои автори класифицират рекурсията като „структурна“ или „генеративна“. Разликата се корени в това, от къде рекурсивното извикване получава данните, с които оперира, и начинът, по който ги обработва.
Функции, които използват списъчни данни, обикновено разделят аргументите на техните преки структурни компоненти и впоследствие ги обработват. Ако някой от тях е от същия тип като входния, функцията е рекурсивна. Поради тази причина, тези функции се определят като (структурно) рекурсивни.
Примери за рекурсия
Опашкова (опашна) рекурсия
При нея рекурсивното обръщение е последното действие, извършвано от викащата подпрограма, преди тя да се върне от своето собствено текущо обръщение.
Това позволява оптимизация, наречена премахване на опашното извикване, т.е. вместо с обръщение към подпрограма рекурсивното обръщение се реализира с обикновен преход (скок) без връщане.
При това текущият кадър от стека се използва повторно за аргументите на опашно-рекурсивното обръщение, вместо да се заделя нов.
Така рекурсията може да се превърне в итерация с постоянно количество памет, независещо от дълбочината на рекурсията.
Това намалява разхода на памет и (обикновено) подобрява бързодействието, но може да затрудни откриването на грешки.
int foo (int x, int y)
{
if (y == 0)
return x;
else
return foo(y, x % y);
}
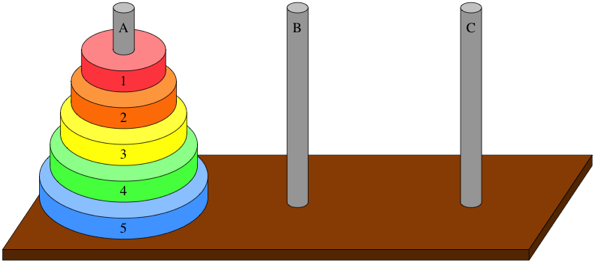
Пример „Ханойска кула“
Ханойската кула е математически пъзел, чието решение илюстрира рекурсията. Има три колчета, които държат дискове с различни диаметри. Голям диск не може да бъде сложен върху по-малък. Започвайки от n дискове на един кол, те трябва да бъдат преместени върху друг едно по едно. Какъв е най-малкият брой стъпки, с който можем да ги преместим?
public void move(int n, int from, int to, int via) {
if (n == 1) {
System.Console.WriteLine("Move disk from pole " + from + " to pole " + to);
} else {
move(n – 1, from, via, to);
move(1, from, to, via);
move(n – 1, via, to, from);
}
}
Пример „Двоично търсене“
Двоичното търсене е метод за намиране на елемент от подреден масив, като го разделяме на половина. На всяка стъпка от двоичното търсене ще проверявате дали на m-та позиция (където m е средата на текущо разглеждания интервал) стои числото m. Ако не, то липсващото число е или на тази позиция, или наляво. Ако ли е, то значи липсващото число е на индекс, по-голям от m.

рекурсия или итерация

– приликите между рекурсия и итерация
* И двете са техники за решаване на проблем.
* Рекурсия и итерация могат да се използват за решаване на проблеми с програмирането.
– разликата между рекурсия и итерация
Ключова разлика – рекурсия срещу итерация
* рекурсията е механизъм за извикване на функция в рамките на една и съща функция, докато итерацията е да се изпълняват множество инструкции многократно, докато даденото условие е вярно
Published: Mar 23, 2022
Latest Revision: Mar 23, 2022
Ourboox Unique Identifier: OB-1299645
Copyright © 2022