by rana
Artwork: رنا عسلي
Copyright © 2017
قانون فيتاغورس

by rana
Artwork: رنا عسلي
- Joined Dec 2016
- Published Books 2
Copyright © 2017
قانون (نظرية) فيتاغورس
واحدة من النظريات الأساسية في المثلثات هي مبرهنة فيثاغورس والتي تنص على أنه في المثلث القائم، مربع طول الوتر (c) يساوي مجموع مربعي طولي الضلعين القائمين (a, b)، أي:
برهان قانون فيتاغورس
هنالك براهين عدة لقانون فيتاغورس، نذكر احدها:
البرهان:
لنعتبر مثلثا قائم الزاوية حيث قياسات أضلاعه هي b ،a و c. نقوم بنسخ المثلث ثلاث مرات بحيث يشكل كل ضلع طوله a مستقيما مع ضلع طوله b لمثلث آخر. نحصل في الأخير على مربع طول ضلعه a+b، كما مبين في الصورة.
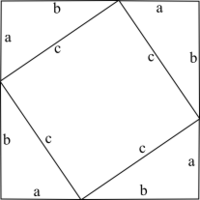
لنحسب مساحة المربع المحدد بالأضلاع ذات الطول c. بالطبع المساحة هي c²، وتساوي أيضا فرق مساحة المربع الكبير ذو الضلع a+b ومجموع مساحات المثلثات الأربع. مساحة المربع الكبير هي ²(a+b) لأن طول ضلعه هو a+b. ومجموع مساحات المثلثات هي أربع مرات مساحة مثلث واحد، أي 4(ab/2)، إذن الفرق هو (a+b)²-4(ab/2) بالتبسيط a²+b²+2ab-2ab أي a²+b². بهذا نكون قد برهنا على أن مساحة المربع ذو الضلع c تساوي a²+b²، أي a²+b²=c².
وهو المطلوب برهانه.

اسئلة على قانون فيتاغورس
السؤال الاول:
لكلّ واحد من المثلّثات القائمة, جد قيمة x بيّن طريقةالحلّ.

السؤال الثاني:
معطى :
مستطيل ABCD و 30 سم = ِAB،
النسبة بين BD و AB هي 17:15.
أ. جد طول BC.
ب. جد مساحة المستطيل.

للمزيد من الاسئلة اضغط هنا.
Published: Feb 1, 2017
Latest Revision: Feb 1, 2017
Ourboox Unique Identifier: OB-236705
Copyright © 2017









