Степенева функція
by Tetyana Masych
Artwork: Тетяна Масич
- Joined Jun 2023
- Published Books 20
Copyright © 2023
Зміст
1. Теоретичні відомості……………………………………….3 – 14
2. Приклади розв’язування типових завдань…….15 – 22
3. Тести………………………………………………………………….23
4. Підготовка до НМТ з математики…………………….24
5.Відео…………………………………………………………………..25 – 26
6. Завдання для самостійної роботи…………………..27 – 28
Теоретичні відомості
Корінь n-гo степеня
Означення: коренем n – го степеня з числа а називається число, n – й степінь якого дорівнює а.
Означення: арифметичним коренем n-го степеня із невід’ємного числа а називається таке невід’ємне число, n-й степінь якого дорівнює а.
Арифметичний корінь п-го степеня із числа а позначають так: ![{\displaystyle {\sqrt[{n}]{a}}=b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a689688935f6bb305cb30a3f4d178cc01d49bb9)
Корінь парного степеня існує лише з невід’ємних чисел.
Корінь непарного степеня існує з будь-якого дійсного числа і до того ж тільки один.
Рівняння виду хn = а
1. У випадку коли a > 0, n ∈ N, n >1:
1) якщо n – парне число, то рівняння має два корені;
2) якщо n – непарне число, то рівняння має один корінь.
2. У випадку а = 0, то рівняння має один корінь: х = 0.
3. У випадку коли а < 0, n ∈ N, n >1:
1) якщо n – парне число, то рівняння не має коренів;
2) якщо n – непарне число, то рівняння має один корінь.
Степенева функція, її властивості та графік
Означення: функція, яка задається формулою y=хn
називається степеневою.
1. Якщо n – парне натуральне число, то графік функції набуває вигляд параболи.
Властивості:
1. Область визначення D(х): х є R.
2. Область значень E(х): у ≥ 0.
3. Функція y=хn – парна.
Означення: Графік парної функції симетричний відносно осі Оу.
4. Функція спадає на проміжку ( – ∞; 0].
5. Функція зростає на проміжку [0; + ∞).
2. Якщо n – непарне натуральне число, то графік функції набуває вигляд кубічної параболи.
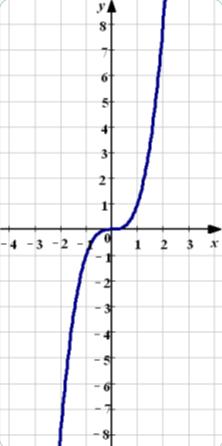
Властивості:
1. Область визначення D(х): х є R.
2. Область значень E(х): у є R.
3. Функція y=хn – непарна.
Означення: Графік непарної функції симетричний відносно початку координат – точки О.
4. Функція зростає на проміжку ( – ∞; + ∞).
3. Якщо n – ціле від’ємне число, коли n – парне , то графік функції набуває вигляду:
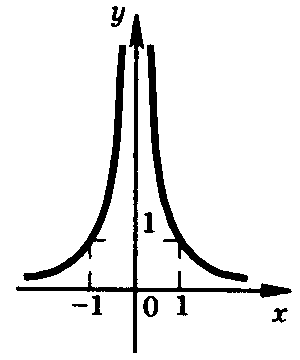
Властивості:
1. Область визначення D(х): х ≠ 0.
2. Область значень E(х): у > 0.
3. Функція y=хn – парна.
4. Функція зростає на проміжку ( – ∞; 0).
5. Функція спадає на проміжку (0; + ∞).
4. Якщо n – ціле від’ємне число, коли n – непарне , то графік функції набуває вигляд гіперболи:
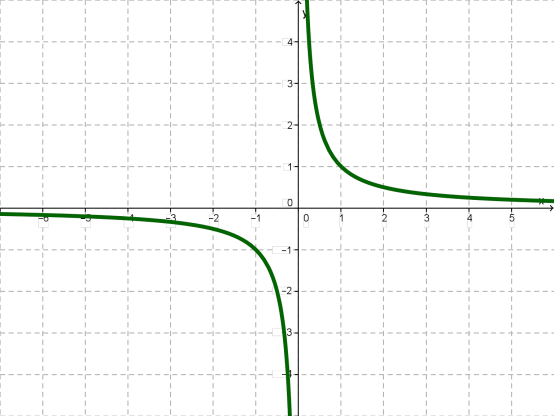
Властивості:
1. Область визначення D(х): х ≠ 0.
2. Область значень E(х): у ≠ 0.
3. Функція y=хn – непарна.
4. Функція спадає на проміжку ( – ∞; 0).
5. Функція спадає на проміжку (0; + ∞).
5. Якщо n – додатне дійсне неціле число, то графік функції набуває вигляду:
коли n < 1 коли n > 1
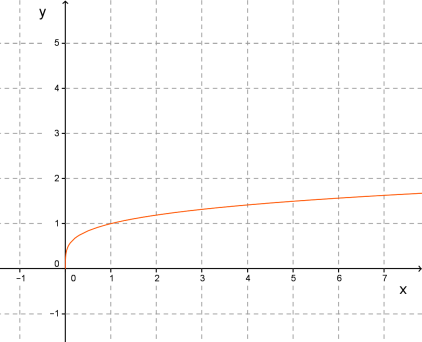
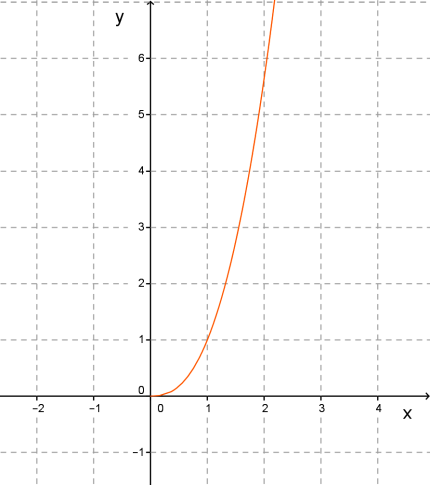
Властивості:
1. Область визначення D(х): х ≥ 0.
2. Область значень E(х): у ≥ 0.
3. Функція зростає на проміжку [0; + ∞).
6. Якщо n – від’ємне дійсне неціле число, то графік функції набуває вигляду:
Властивості:
1. Область визначення D(х): х > 0.
2. Область значень E(х): у > 0.
3. Функція спадає на проміжку (0; + ∞).
Тести
1. Виконайте тести за посиланням:
https://vseosvita.ua/test/start/gco771
2. Виконайте інтерактивну вправу:
Підготовка до НМТ з математики
Виконайте завдання з теми за посиланням:
https://zno.osvita.ua/mathematics/tag-pokaznykovi_logharyfmichni_tryghonometrychni_funkciyi/
Відео
Перегляньте навчальне відео:
Published: Jul 31, 2023
Latest Revision: Jul 31, 2023
Ourboox Unique Identifier: OB-1482350
Copyright © 2023
