
Елементи теорії ймовірностей і математичної статистики

by Tetyana Masych
Artwork: Тетяна Масич
- Joined Jun 2023
- Published Books 20
Copyright © 2023

Зміст
1. Теоретичні відомості……………………………………….3 – 12
2. Приклади розв’язування типових завдань…….13 – 20
3. Тести………………………………………………………………….21
4. Підготовка до НМТ з математики…………………….22
5.Відео…………………………………………………………………..23 – 26
6. Завдання для самостійної роботи…………………..27 – 28
Теоретичні відомості
Означення: Комбінаторика – розділ математики, у якому вивчають способи вибору та розташування елементів з деякої скінченої множини відповідно до заданих правил.
Багато комбінаторних задач можна розв′язати за допомогою двох важливих правил, які називаються правило суми і правило добутку.
Правило суми: якщо деякий об’єкт А можна вибрати m способами, а інший об’єкт В можна вибрати n способами, то вибір “Або А, або В” можна здійснити m+n способами.
Правило добутку: якщо деякий об’єкт А можна вибрати m способами і після кожного такого вибору інший об’єкт В можна вибрати n способами, то вибір пари (А; В) у вказаному порядку можна здійснити mn способами.
Важливим у комбінаториці є поняття факторіала.
Означення: добуток всіх натуральних чисел від 1 до n, де
n – ціле невід’ємне число, називається факторіалом числа n і записується n! (читається, як “ен факторіал”).
n!=1⋅2⋅3⋅…⋅(n−2)⋅(n−1)⋅n
Означення: перестановкою з n елементів називається будь-яка впорядкована множина, що складається з усіх цих n елементів.
Перестановки відрізняються одна від одної лише порядком елементів.
Pn = n!
Означення: розміщенням з n елементів по m (де m ≤ n) називається будь – яка впорядкована підмножина з m елементів даної множини М, що містить n елементів. Розміщення відрізняються один від одного або елементами, або їх порядком.
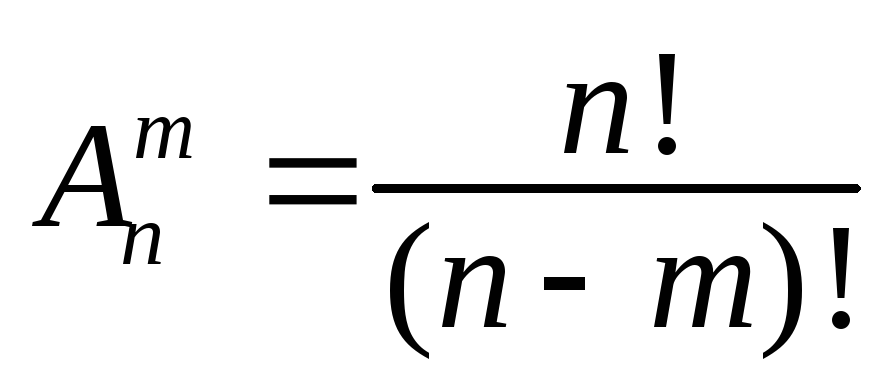
Означення: комбінацією з n елементів по m (де m ≤ n) називається будь – яка не впорядкована підмножина з m елементів даної множини М, що містить n елементів.
Комбінації відрізняються лише складом елементів. Порядок елементів у множині неістотний.

Комбінація відрізняється від розміщення тим, що у цій підмножині неістотним є порядок елементів.

Вибір формули для обчислення кількості сполук

Означення: Теорія ймовірностей – математична наука, що вивчає закономірності випадкових явищ.
Якщо проводяться певні досліди, підсумок яких передбачити неможливо, то такі досліди в теорії ймовірностей називають випадковими.
Означення: випадковий дослід – це дослід, результат якого залежить від випадку і який можна повторювати багато разів за одних і тих самих умов.
Результатом випадкового досліду є випадкова подія.
Означення: випадкова подія – це подія, яка за одних і тих самих умов може відбутися, а може і не відбутися.
Означення: подія, яка за даних умов обов’язково відбудеться, називається вірогідною (або достовірною).
Означення: подія, яка за даних умов ніколи не відбудеться, називається неможливою.
Означення: дві події називаються сумісними, якщо поява однієї з них не виключає появу другої події в тому самому випробуванні.
Означення: дві події називаються несумісними, якщо поява однієї з них виключає появу іншої події в даному випробуванні.
Означення: рівноймовірними називаються події, ймовірності яких однакові в даному випробуванні.
Класичне означення ймовірності: ймовірність події А дорівнює відношенню кількості випадків m, що сприяють появі події А, до кількості всіх можливих випадків n.
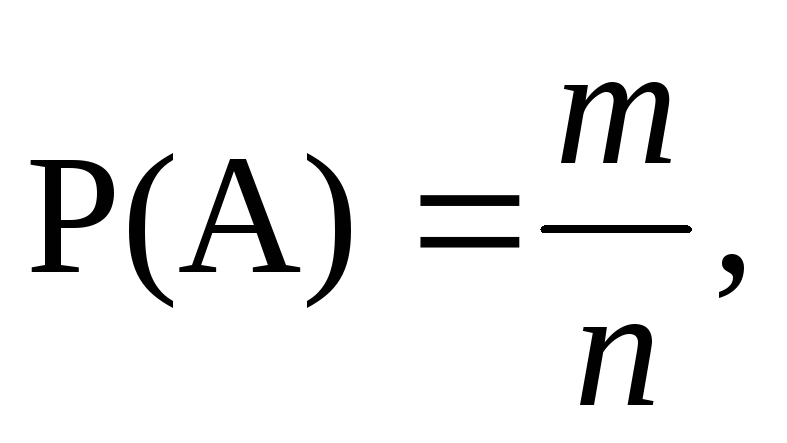
Ймовірність вірогідної події дорівнює 1; ймовірність неможливої події дорівнює 0; ймовірність випадкової події може бути будь – яким числом від 0 до 1.
Означення: Математична статистика – розділ математики, у якому вивчають методи збирання, систематизації, обробки та дослідження статистичних даних для наукових і практичних висновків.
Означення: генеральна сукупність – це сукупність усіх об’єктів, що підлягають дослідженню.
Означення: вибіркою називають сукупність об’єктів, вибраних випадковим чином з генеральної сукупності.
Означення: варіанта – одне із значень елементів вибірки.

Означення: операцію розташування випадкових величин вибірки за принципом неспадання називають ранжуванням вибірки.
Вибіркові характеристики:
Означення: розмах вибірки R – це різниця між найбільшим і найменшим значенням випадкової величини у вибірці.
Означення: мода вибірки Мо – це значення випадкової величини, яке трапляється у вибірці найчастіше.
Означення: медіана вибірки Ме – це серединне значення ранжованої вибірки.
Означення: середнє значення вибірки Х – це середнє арифметичне всіх її значень.
Графічне подання інформації про вибірку
Результати статистичних досліджень після обробки можна подати у наочній і компактній формі.
Означення: полігоном частот називають ламану лінію, відрізки якої послідовно сполучають точки з координатами
(х1;n1); (х2;n2) ,…, (хk;nk), де хj – значення випадкової величини, nj – відповідні їм частоти.


Приклади розв’язування типових завдань
Задача 1: У вазі лежать три яблука та чотири груші. Скількома способами можна обрати один фрукт?
Розв’язання:
Якщо у вазі лежать 3 яблука, то одне яблуко можна обрати трьома способами (можемо взяти одне із 3 яблук). Якщо у вазі лежать 4 груші, то одну грушу можна обрати чотирма способами (можемо взяти одну із чотирьох груш). А обрати один фрукт можна 3+4=7 способами.
Відповідь: 7 способів
Задача 2: Скількома способами можна вибрати голосну та приголосну літери зі слова “приклад”?
Розв’язання:
Голосну літеру можна вибрати 2 способами (можна взяти одну з літер “а” або “и”). Приголосну літеру можна вибрати 5 способами (можна взяти одну із літер “п”, “р”,”к”, “л”, “д”). Для кожного з 2 способів вибору голосної літери є 5 способів вибору приголосної літери. Тому пару із голосної та приголосної літер можна вибрати 2·5=10 способів.
Відповідь: 10 способів
Задача 3: Обчисліть 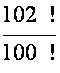 .
.
Розв’язання:
Спростимо обчислення. Факторіал числа 102 за означенням дорівнює 102! = 1 · 2 · …· 99 · 100 · 101 · 102.
За виглядом знаменника виділимо із записаного добутку 100! і отримаємо
102! = (1 · 2 · …· 99 · 100) · 101 · 102 = 100! · 101 · 102
За означенням факторіал будь – якого цілого невід’ємного числа є натуральним числом, тобто не дорівнює нулю.
Тоді 100! ≠ 0, а отже на нього можна скоротити чисельник і знаменник:
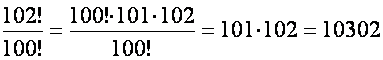
Відповідь: 10302
Задача 4: Скількома способами можна розсадити 8 студентів в ряд з 8 місць?
Розв’язання:
Маємо справу з перестановкою, а тому використовуємо формулу:
![]() .
.
Відповідь: 40320 способів
Задача 5: В класі 10 навчальних предметів і 5 різних уроків в день. Скількома способами можна розподілити уроки на день.
Розв’язання:
Для нас важливий порядок предмету в розкладі.
Тому всі можливі розподіли уроків на день являють собою, розміщення з 10 елементів по 5.
Отже, всіх способів розподілу повинно бути: ![]()
Відповідь: 30240 способів
Задача 6: Скількома способами можна вибрати двох чергових із групи 17 чоловік?
Розв’язання:
У задачі неважливий порядок розміщення здобувачів освіти у групі, а лише кількість різних груп.
Тому застосовуємо формулу комбінацій С з 17 по 2:
C172=17!/(17-2)!/2!=17 · 16/2=136.
Отже, можемо скласти 136 різних пар з двох чергових.
Відповідь: 136 способів
Задача 7: У ящику 16 синіх і 12 білих кульок. Яка ймовірність витягнути з ящика синю кульку?
Розв’язання:
Формула для знаходження ймовірності ![]()
n = 18 + 12 = 30; m = 18;
Р(А) = 18/30 = 0,6
Відповідь: Р(А) = 0,6
Задача 8: Відділ технічного контролю серед 100 виробів виявив 8 нестандартних. Знайдіть ймовірність появи нестандартних виробів.
Розв`язання: Позначимо через А таку подію, як поява нестандартного виробу. Тоді одержимо:
Р (A) = = 0,08.
Відповідь: Р (A) = 0,08.
Задача 9: Знайдіть імовірність одночасного випадання герба на двох монетах при одному киданні двох монет.
Розв’язання:
Подія А – «випав герб на першій монеті», Р(А) = ⅟₂.
Подія В – «випав герб на другій монеті», Р(В) = ⅟₂.
Оскільки поді А і В незалежні, то
Р(А · В) = Р(А) · Р(В) = ⅟₂ · ⅟₂ = ⅟₄
Відповідь: ⅟₄
Задача 10: У шкільній олімпіаді з математики взяли участь 20 здобувачів освіти. Бали, набрані учасниками олімпіади подано у вигляді таблиці. Знайдіть розмах, моду, медіану, середнє значення вибірки.
|
Бал |
5 |
7 |
9 |
10 |
12 |
15 | 16 |
18 |
|
Частота балів |
3 |
4 | 2 | 1 | 5 | 3 | 1 |
1 |
Розв’язання:
R = 18 – 5 = 13
Мо = 12
Ме = (10 + 12) : 2 = 11
Х = ( 5·3 + 7·4 + 9·2 + 10 + 12·5 + 15·3 + 16 + 18) : 20 = 210 : 20 = 10,5
Відповідь: R = 13; Мо = 12; Ме = 11; Х = 10,5.


Тести
1. Виконайте тести за посиланням:
https://vseosvita.ua/test/start/xdy890
2. Пройдіть вебквест за посиланням:
https://vseosvita.ua/webquest/start/s/2852/319583-fac31642

Підготовка до НМТ з математики
Виконайте завдання за посиланням:
Перестановки, комбінації, розміщення. Комбінаторні правила суми та добутку:
https://zno.osvita.ua/mathematics/tag-kombinatorni_pravila/
Ймовірність випадкової події. Вибіркові характеристики:
https://zno.osvita.ua/mathematics/tag-jmovirnist_vypadkovoyi_podiyi/

Відео
Перегляньте навчальне відео:
Завдання для самостійної роботи
Завдання 1:
Вкажіть, яка це подія:
1) вночі світить сонце
2) 1 січня – святковий день
3) опівночі випаде сніг, а через 24 години буде світити сонце
4) при підкиданні грального кубика випало 7 очок
5) при підкиданні грального кубика випало число очок, менше 7
6) при телефонному дзвінку абонент виявився зайнятий
7) при підкиданні грального кубика випало 2 очки
8) навчальний рік коли-небудь закінчиться
9) бутерброд впаде маслом вниз
10) ви виграєте, беручи участь у лотереї
11) 30 лютого буде дощ
12) завтра сонце зійде на заході
13) влітку у школярів канікули будуть
14) при підкиданні грального кубика випало парне число очок
15) 1 липня в Одесі буде сонячно
16) після четверга буде п’ятниця
17) день народження мого друга – число, менше ніж 32
Завдання 2:
Розв’яжіть задачу:
При підкиданні грального кубика обчисліть ймовірність таких подій:
А: випало парне число очок;
В: випало число очок кратне трьом.
Published: Jul 10, 2023
Latest Revision: Jul 10, 2023
Ourboox Unique Identifier: OB-1476238
Copyright © 2023







