
Паралельність прямих і площин у просторі

by Tetyana Masych
Artwork: Тетяна Масич
- Joined Jun 2023
- Published Books 20
Copyright © 2023

Зміст
1.Теоретичні відомості…………………………………………3 – 10
1.1.Паралельність прямих у просторі………………….3 – 4
1.2.Паралельність прямої і площини у просторі…5 – 7
1.3.Паралельність площин у просторі………………….8 – 10
2.Приклади розв’язування завдань……………………..11 – 18
3.Тести……………………………………………………………………19 – 20
4.Підготовка до НМТ з математики………………………21
5.Відео……………………………………………………………………22 – 23
6.Завдання для самостійної роботи……………………..24

Паралельність прямих у просторі
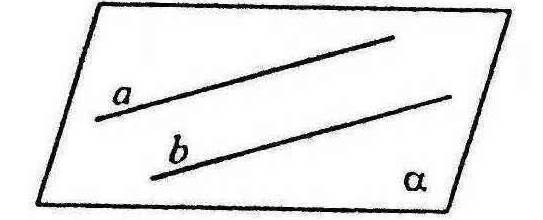
Означення: Дві прямі в просторі називаються паралельними, якщо вони лежать в одній площині та не перетинаються.
Паралельність прямих a і b позначається так: a∥b або b∥a.

Ознака паралельних прямих:
Дві прямі, паралельні третій, паралельні між собою.
Теорема 1: Через дві паралельні прямі можна провести площину, і до того ж тільки одну.
Теорема 2: Через будь-яку точку простору поза даною прямою можна провести пряму, паралельну даній прямій, і до того ж тільки одну.
Теорема 3: Якщо одна з двох паралельних прямих перетинає дану площину, то й інша пряма перетинає цю площину.

Пам’ятайте, що у просторі справджуються всі властивості паралельних прямих, які ви вивчали у планіметрії.
Паралельність прямої і площини у просторі
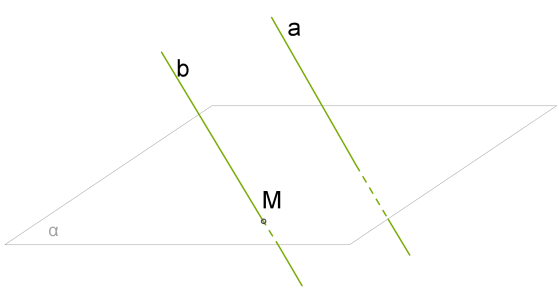
Означення: Пряма і площина називаються паралельними, якщо вони не мають спільних точок.
Ознака паралельності прямої і площини:
Якщо пряма, що не лежить у даній площині, паралельна будь-якій прямій з цієї площини, то ця пряма паралельна даній площині.

Наслідок 1: Якщо пряма паралельна площині, то в цій площині через задану точку можна провести лише одну пряму, паралельну даній.
Наслідок 2: Через точку поза площиною можна провести безліч прямих, паралельних даній площині.
Наслідок 3: Якщо пряма належить одній площині і паралельна до лінії перетину її з другою площиною, то ця пряма паралельна другій площині.
Наслідок 4: Через точку поза площиною можна провести безліч прямих паралельних даній площині, але тільки одну пряму, паралельну заданій прямій з цієї площини.

Теорема: Якщо одна з двох паралельних прямих перетинає площину, то і друга пряма також перетинає цю площину.


Паралельність площин у просторі
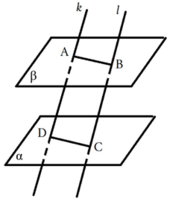
Означення: Дві площини називаються паралельними, якщо вони не перетинаються.
Паралельні площини α і β позначаються α∥β.

Ознака паралельності площин: Якщо дві прямі, що перетинаються, однієї площини відповідно паралельні двом прямим, що перетинаються, другої площини, то ці площини паралельні.

Властивості паралельних площин:
Теорема 1: Якщо дві паралельні площини перетинаються третьою, то прямі перетину паралельні.

Теорема 2: Відрізки паралельних прямих, які містяться між паралельними площинами, рівні.

Приклади розв’язування завдань
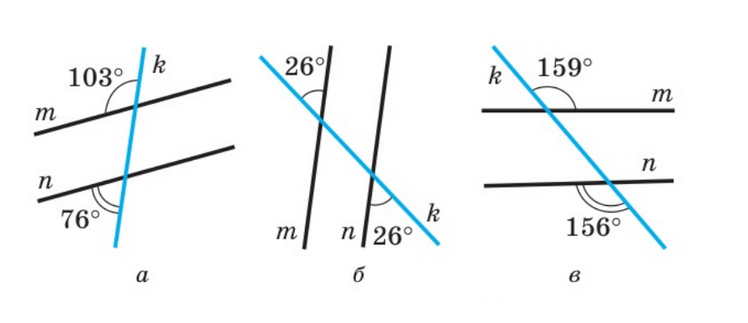
Задача 1: Вкажіть на якому з малюнків зображено паралельні прямі.
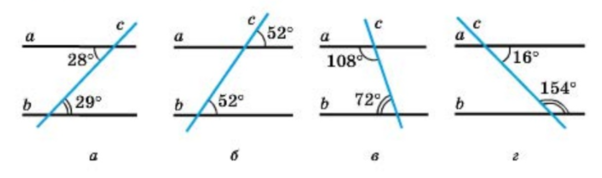
Розв’язання:
а) Не паралельні.
б) Паралельні.
в) Паралельні.
г) Не паралельні.

Необхідно згадати властивості кутів, утворених при перетині двох паралельних прямих січною.

Задача 2:
Дано: SА1: SА = SВ1: SВ = SС1: SС
Довести: ( А1В1С1 ) ∥ (АВС)
Доведення:
Розглянемо кут АSВ.
Оскільки SА1: SА = SВ1: SВ, то А1В1 ∥ АВ (за теоремою Фалеса).
Аналогічно доводимо, що В1С1 ∥ ВС.
Тоді А1В1 ꓵ В1С1 і АВ ꓵ ВС відповідно паралельні.
Отже, ( А1В1С1 ) ∥ (АВС) за ознакою паралельності площин.
Задача 3:
Дано: паралелограми АВЕD і АСFD лежать у різних площинах
Довести: ВСFЕ – паралелограм
Доведення:
АD ∥ ВЕ і АD = ВЕ, тому що АВЕD – паралелограм.
АD ∥ СF і АD = СF, тому що АСFD – паралелограм.
Тому ВЕ ∥ СF і ВЕ = СF.
Отже, ВСFЕ – паралелограм.

Задача 4:
У просторі задано паралельні прямі m і n. Які з наведених тверджень є правильними?
І. Існує площина, що містить обидві прямі m і n.
ІІ. Існує пряма, що перетинає обидві прямі m і n.
ІІІ. Існує точка, що належить обом прямим m і n.
Розв’язання:
І. Оскільки в просторі прямі називаються паралельними, якщо вони не перетинаються і лежать в одній площині, то така площина існує. Є правильним.
ІІ. Так як прямі паралельні, то вони лежать в одній площині. А на площині завжди є пряма, що перетинає паралельні прямі. Є правильним.
ІІІ. Оскільки в просторі прямі називаються паралельними, якщо вони не перетинаються і лежать в одній площині, то вони не мають спільної точки. Не є правильним.
Задача 5:

На рисунку зображено куб ABCDA1B1C1D1. Яка з наведених прямих паралельна площині (AA1B1)?
| А | Б | В | Г | Д |
| BC | BD | C1D | CB1 | A1B |
Розв’язання:
А) пряма перетинає площину; Б) пряма перетинає площину; В) пряма паралельна площині (вона паралельна прямій B1А, що лежить в цій площині); Г) пряма перетинає площину;
Д) пряма лежить в площині.
Відповідь: В.

Тести
1)Виконайте тести за посиланням:
https://vseosvita.ua/test/start/lhw201
2)Виконайте інтерактивну вправу:
Підготовка до НМТ з математики
Виконайте завдання за посиланням:
https://zno.osvita.ua/mathematics/tag-pryami_ta_ploshini_u_prostori/

Відео
Перегляньте відео :
Завдання для самостійної роботи
1.Вкажіть на якому з малюнків зображено паралельні прямі.
2.Перегляньте відео за посиланням і виконайте завдання.

Published: Jun 20, 2023
Latest Revision: Jun 20, 2023
Ourboox Unique Identifier: OB-1469939
Copyright © 2023







