Ознаки рівності трикутників

by MarianaTymkiw

Artwork: Тимків Мар'яна Ігорівна

Joined Nov 2022
Published Books 1

Ознайомтеся із матеріалом та виконайте завдання

2

Зміст

1.Рівність геометричних фігур

2.Перша ознака рівності трикутників

3.Друга ознака рівності трикутників

4.Види трикутників.Рівнобедрений трикутник, його властивості та ознаки

5.Медіана, бісектриса і висота трикутника

6.Третя ознака рівності трикутників

7.Ілюстровані задачі

3

Рівність геометричних фігур

Фігури, які можна сумістити накладанням одна на одну, називаються рівними.

Якщо кожна з двох фігур рівна третій фігурі, то перші дві фігури рівні.

Для будь-якого трикутника існує рівний йому трикутник у заданому розташуванні щодо заданого променя.

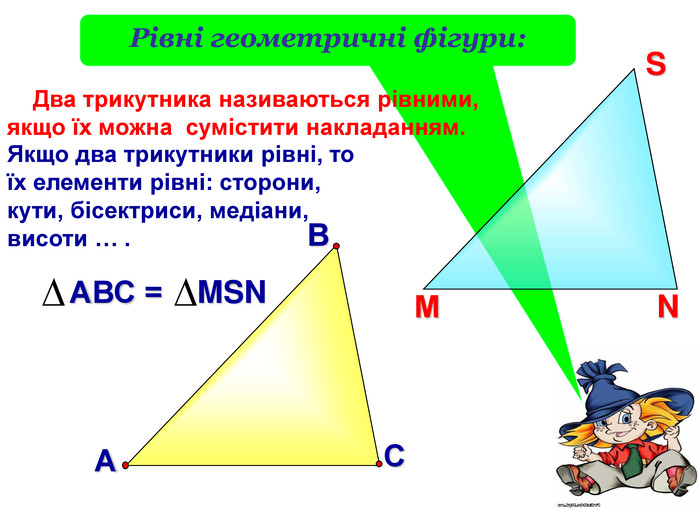
Презентація до уроку геометрії у 7 класі "Рівність геометричних фігур" Презентація до уроку "Рівність фігур"

Рівні трикутники мають рівні відповідні кути й рівні відповідні сторони.

4

Перша ознака рівності трикутників

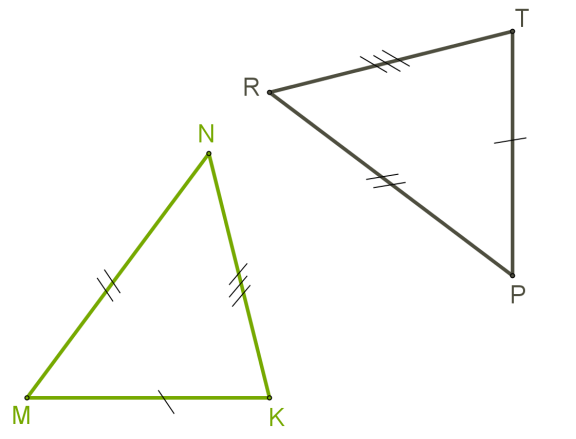
Якщо дві сторони і кут між ними одного трикутника відповідно дорівнюють двом сторонам і куту між ними іншого трикутника, то такі трикутники рівні.

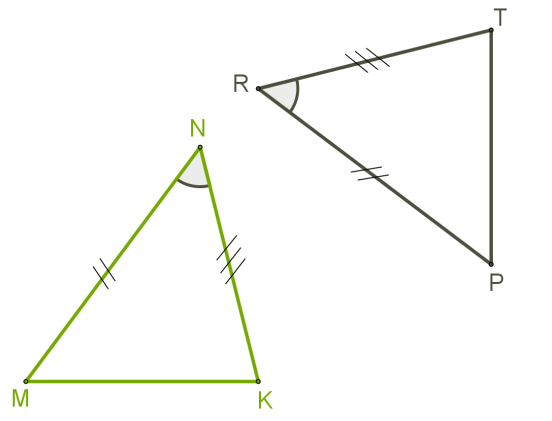
MN=PR
KN=TR
∠N=∠R

Чи достатньо цієї інформації для доведення рівності трикутників? Чи можна накласти фігури одна на одну?

1. Оскільки ∠N=∠R, то ΔMNK можна накласти на ΔPRT так, що вершина N суміститься з вершиною R, а сторони NM і NK сумістяться, відповідно, з променями RP і RT.

2. Оскільки MN=PR,KN=TR, то сторона MN суміститься зі стороною PR, а сторона KN — зі стороною TR. Зокрема, сумістяться точки M і P, K і T.

Сумістяться сторони MK і PT. Отже, ΔMNK і ΔPRT повністю накладаються, тому вони рівні.

5

Друга ознака рівності трикутників

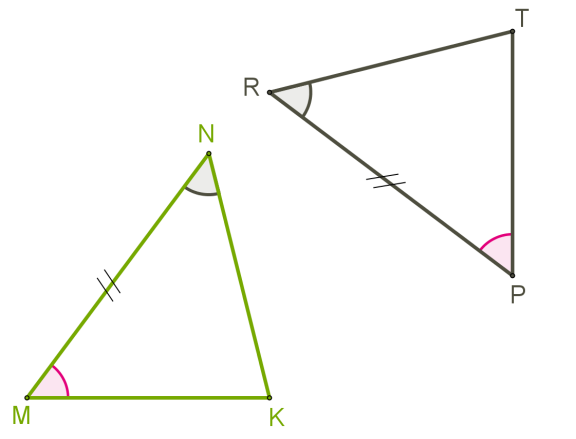
Якщо сторона і два прилеглих до неї кути одного трикутника відповідно дорівнюють стороні та двом прилеглим до неї кутам іншого трикутника, то такі трикутники рівні.

MN=PR

∠N=∠R

∠M=∠P

Як і при доведенні першої ознаки, потрібно переконатися, чи достатньо цих даних для рівності трикутників. Чи можна накласти трикутники один на одний?

1. Оскільки MN=PR, то ці відрізки накладаються, якщо поєднати їхні кінцеві точки.

2. Оскільки ∠N=∠R і ∠M=∠P, то промені MK і NK накладуться відповідно на промені PT і RT.

3. Якщо збігаються промені, то збігаються точки їх перетину K і T.

4. Поєднано всі вершини трикутників, тобто ΔMNK і ΔPRT повністю накладаються. Отже, трикутники рівні.

6

Види трикутників.Рівнобедрений трикутник, його властивості та ознаки

Трикутник, у якого всі сторони різні,називається різностороннім.

У задачах часто зустрічається трикутник із рівними сторонами. Такі трикутники мають особливі властивості.

Трикутник називається рівнобедреним, якщо в нього дві сторони рівні.

Дві рівні сторони рівнобедреного трикутника називають бічними сторонами, а третя сторона — основою.

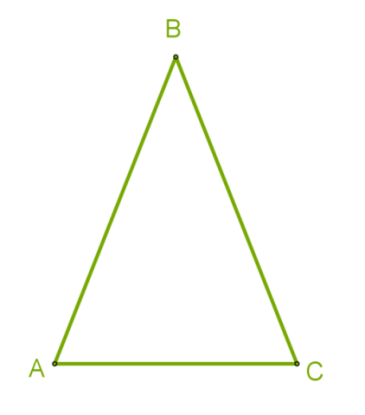На рисунку зображено рівнобедрений трикутник ABC з бічними сторонами AB і BC та основою AC.

7

Рівнобедрений трикутник, його властивості та ознаки

Рівнобедрений трикутник має властивості, яких не мають різносторонні трикутники:

1. У рівнобедренному трикутнику кути, прилеглі до основи, є рівними.

2. У рівнобедренному трикутнику бісектриса, проведена до основи, є медіаною і висотою.

3.У рівнобедренному трикутнику медіана, проведена до основи, є бісектрисою і висотою.

4. У рівнобедренному трикутнику висота, проведена до основи, є бісектрисою і медіаною.

Першу й другу властивості можна довести, якщо доведемо рівність двох трикутників, які утворюються, коли з протилежного до основи кута провести бісектрису BD.

8

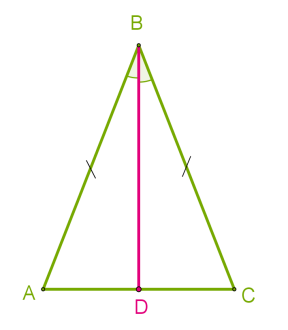
Медіана, бісектриса і висота трикутника

Розглянемо рівнобедрений трикутник ABC з основою AC і доведемо, що ΔABD=ΔCBD.

Нехай BD — бісектриса трикутника ABC.

ΔABD=ΔCBD за першою ознакою рівності трикутників.

1. AB=BC, як бічні сторони рівнобедреного трикутника.

2. BD — спільна сторона.

3. ∠ABD=∠CBD, за властивістю бісектриси.

У рівних трикутників відповідні сторони і відповідні кути рівні:

1. ∠A=∠C — доведено, що прилеглі до основи кути рівні.

2. AD=DC — доведено, що бісектриса є медіаною.

3. ∠ADB=∠CDB — оскільки суміжні кути, сума яких дорівнює 180°, рівні, то кожен із них дорівнює 90°, тобто медіана є висотою.

Ознака рівнобедреного трикутника
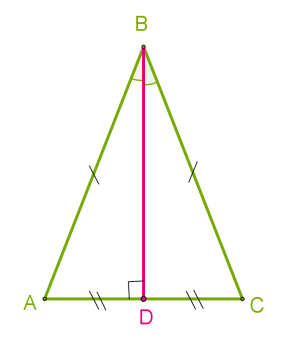
Якщо в трикутнику два кути рівні, то він рівнобедрений.

9

Третя ознака рівності трикутників

Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні.

MN=PR

KN=TR

MK=PT

Спробуємо поєднати трикутники ΔMNK і ΔPRT за допомогою накладання й переконатися, що відповідна рівність сторін гарантує рівність відповідних кутів цих трикутників, і вони повністю збігаються.

1. Сумістимо, наприклад, однакові відрізки MK і PT. Припустимо, що точки N і R при цьому не суміщаються.

2. Нехай O — середина відрізка NR. Відповідно до цієї інформації, MN=PR, KN=TR.

3. Трикутники MNR і KNR — рівнобедрені зі спільною основою NR. Тому їх медіани MO і KO є висотами, отже, вони перпендикулярні до NR.

4. Прямі MO і KO не суміщаються. Точки M, K, і O не лежать на одній прямій. Але через точку O до прямої NR можна провести лише одну перпендикулярну їй пряму.

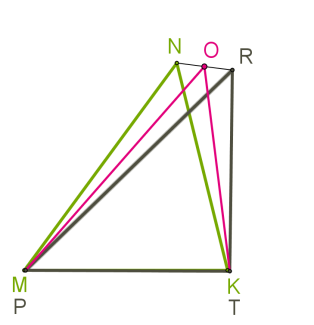
Ми отримали суперечність. Отже, доведено, що повинні поєднатися й вершини N і R.

Третя ознака дозволяє назвати трикутник дуже сильною, стійкою фігурою. Іноді говорять, що трикутник — жорстка фігура. Якщо довжини сторін не змінюються, то кути також не змінюються.

10

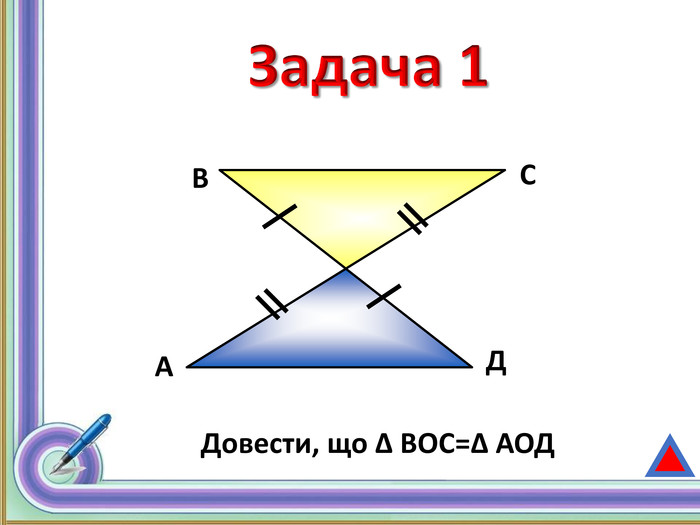
Ілюстровані задачі

Презентація "Ознаки рівності трикутників (задачі за готовими малюнками)"

11

Ознаки рівності трикутників by MarianaTymkiw - Illustrated by Тимків Мар