
Фале́с Міле́тський(623 до н. е.— 546 до н. е., ) — давньогрецький філософ досократського періоду, математик, астроном, засновник іонійської школи натурфілософії, купець і політичний діяч.
Відомо небагато свідчень щодо життя Фалеса, переважно вони мають характер афоризмів. Згідно зі свідченнями Геродота, Дуріса й Демокріта, він походив зі знатного фінікійського роду Фелідів, нащадків легендарних Агенора й Кадма. Батьками Фалеса були Ексамій і Клеобуліна[3][4][5].
Він багато подорожував, зокрема, у молодості відвідав Єгипет, де в школах Мемфіса і Фів вивчав різні науки. Повернувшись на батьківщину, заснував у Мілеті філософську школу. Вважався одним із Семи мудреців. Здобуття слави мудреця пов’язується зі знахідкою в морі золотого триніжника, який за волею оракула (або домовленістю претендентів на нього) мусив бути відданий наймудрішому і таким жителі Мілета визнали Фалеса. За іншою версією, Фалес отримав золотий кубок чи піалу з присвятою наймудрішому та передав її іншим мислителям, які повернули коштовність назад Фалесу[6].
Фалес жив сам і тримався осторонь державних справ. Проте, згідно переказів, він всиновив сина своєї сестри Кібіста[7]. Він не прагнув багатства, проте з метою продемонструвати, що філософ може бути успішним у буденних справах, передбачив урожай маслин та заздалегідь викупив чавильні олії поблизу, отримавши таким чином велику вигоду від здачі їх в оренду[8].
- теорема про рівність вертикальних кутів,
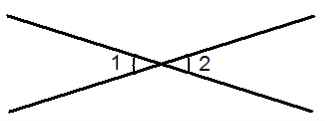
– теорема про рівність кутів при основі рівнобедреного трикутники,
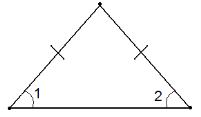
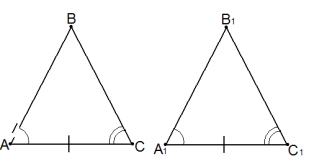 -другої ознаки рівності трикутників-
-другої ознаки рівності трикутників-
-Кут, що спирається на діаметр, прямий.
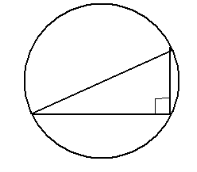
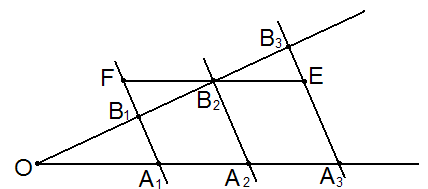
Теорема. Якщо паралельні прямі , що перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на другій стороні кута.
Теорема Фалеса . Якщо паралельні прямі, які перетинають сторони куті, ви бачите на одній сторонній стороні сторонні сторони, при цьому, що ви бачите від своїх війок і на другій стороні.
Якщо паралельні прямі перетинають сторони куті, то відриваються, які закриваються на одній сторонній куті, пропонують довірити, що закривають на другій стороні куті.
Властивість медіану трикутника: всі три медіані трикутника перериваються у своїх точах, які діліть кожну з них при зменшенні 2: 1, використовуючи від вершини трикутника.
Властивість бісектриси трикутника : бісектриса трикутника ділить свою сторону на відривків, пропонуючи прилеглі до них сторонніх
ДЯКУЮ ЗА УВАГУ))) !!!
Published: Nov 27, 2019
Latest Revision: Nov 27, 2019
Ourboox Unique Identifier: OB-691210
Copyright © 2019









