by jalal
Copyright © 2019
نظرية فيثاغورس
Copyright © 2019
نظرية فيثاغورس
مُقدم من قبل:
جلال عبد الرحيم ربحي بشاره
026307652 058995291
مقدم ل:
د. مؤنس طيبي
2019/2020
فيثاغورس (570 – 495 ق.م) هو فيلسوف وعالم رياضيات يوناني، مؤسس الحركة الفيثاغورية كما يُعرف بمعادلته الشهيرة (نظرية فيثاغورس). اتتنا معلومات حوله من كتب كتبت قرون بعد وفاته، لذلك لا يوجد معلومات موثقة حول افكاره واعماله. ولد في جزيرة ساموس وسافر إلى بلاد عديدة منها اليونان ومصر وربما الهند. أقام في مستعمرة كروتوني اليونانية في إيطاليا حوالي سنة 530 ق.م. حيث أنشأ مدرسة لمناقشة موضوعات فلسفية مختلفة من مثل ماذا يحدث للروح عندما يموت الجسد.
واهتم فيثاغورس كثيراً بعدد من المواضيع العلمية والرياضية والموسيقية مثلا، قد بيّن العلاقة بين شد ورخوة السلك والنغمة الموسيقية التي يبعثها عندما يُنقر عليه في فترات منتظمة، وتكون النتيجة سلّما موسيقيا هرمونيا.
هي علاقة أساسية في الهندسة الإقليدية بين أضلاع المثلث قائم الزّاوية
الشكل الأكثر شهرة لنظرية فيثاغورس:
« في مثلث قائم الزاوية، مربع طول الوتر يساوي مجموع مربعي طولي الضلعين المحاذيين للزاوية القائمة. »
الصيغة العامة للنظرية هي:
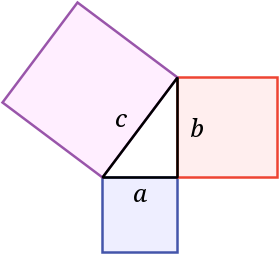
الصيغة الهندسية لنظرية فيثاغورس. مجموع مساحة المربعين الواقعين على الضلعين a و b يساوي مساحة المربع الواقع على الضلع c |
برهان اخر
للمشاهدة
ثلاثية فيثاغورس
تألف ثلاثية فيثاغورس من الأعداد الصحيحة a و b و c حيث [a2 + b2 = c2]
تكتب الثلاثية على الشكل (a, b, c) ومن الأمثلة الشهيرة عليها هي (5, 4, 3). إذا كانت (a, b, c) هي ثلاثية فيثاغورسية فإن (ka, kb, kc) من أجل أي عدد صحيح k تكون أيضاً ثلاثية فيثاغورسية. تكون الأعداد المشكلة لثلاثية فيثاغورس a, b و c أولية فيما بينها.
تم أخذ الاسم من مبرهنة فيثاغورس حيث تكون كل ثلاثية فيثاغورس حلاً لمبرهنة فيثاغورس.
هناك ست عشر ثلاثية فيثاغورس حيث c ≤ 100:
| (6 , 8 , 10) | ( 3 , 4 , 5 ) | ( 5, 12, 13) | ( 7, 24, 25) | ( 8, 15, 17) |
| ( 9, 40, 41) | (11, 60, 61) | (12, 35, 37) | (13, 84, 85) | |
| (16, 63, 65) | (20, 21, 29) | (28, 45, 53) | (33, 56, 65) | |
| (36, 77, 85) | (39, 80, 89) | (48, 55, 73) | (65, 72, 97) |
Published: May 21, 2019
Latest Revision: May 21, 2019
Ourboox Unique Identifier: OB-632821
Copyright © 2019
Skip to content