في الرياضيات، نظرية فيثاغورس أو مبرهنة فيثاغورس :  هي نظرية في الهندسة الإقليدية، تنص على أنه في أي مثلث قائم الزاوية يكون مجموع مربع طول الضلعين المحاذيين للزاوية القائمة مساويا لمربع طول الوتر. سميت هذه المبرهنة هكذا نسبة إلى العالم فيثاغورس الذي كان رياضيا وفيلسوفاوعالم فلك في اليونان القديمة.

نظرية فيثاغورس المباشرة

وهي الشكل الأكثر شهرة لنظرية فيثاغورس:

« في مثلث قائم الزاوية، مربع طول الوتر يساوي مجموع مربعي طولي الضلعين المحاذيين للزاوية القائمة. »

في مثلث ABC قائم الزاوية في C، أي أن [AB] هو الوتر، نضع AB=c و AC=b و BC=a. لدينا:

 BC^{2}+AC^{2}=AB^{2},}

أو

 a^{2}+b^{2}=c^{2},}

تمكن نظرية فيثاغورس من حساب طول أحد أضلاع مثلث قائم الزاوية بمعرفة طولي الضلعين الآخرين. مثلا: إذا كان b=3 و a=4 فإن

 a^{2}+b^{2}=3^{2}+4^{2}=25=c^{2},}

ومنه c=5,}.

أي ثلاثة أعداد صحيحة تمثل أطوال أضلاع مثلث قائم الزاوية -مثل (3، 4، 5)- تُكون ثلاثي فيثاغورسي

نظرية فيثاغورس العكسيه

« في مثلث، إذا كان مربع طول أطول ضلع يساوي مجموع مربعي طولي الضلعين الآخرين، فإن هذا المثلث قائم الزاوية. الزاوية القائمة هي الزاوية المقابلة لأطول ضلع، والضلع الأطول هو الوتر. »

نظرية فيثاغورس هي خاصية مميزة للمثلث القائم الزاوية. بتعبير آخر:

« في مثلث ABC، إذا كان AC²+BC²=AB² فإن هذا المثلث قائم الزاوية في C.».

برهان حديث

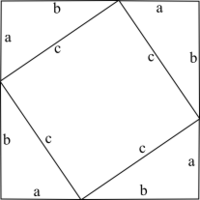لنعتبر مثلثا قائم الزاوية حيث قياسات أضلاعه هي b ،a و c. نقوم بنسخ المثلث ثلاث مرات بحيث يشكل كل ضلع طوله a مستقيما مع ضلع طوله b لمثلث آخر. نحصل في الأخير على مربع طول ضلعه a+bb، كما في الصورة.

لنحسب مساحة المربع المحدد بالأضلاع ذات الطول c. بالطبع المساحة هي c²، وتساوي أيضا فرق مساحة المربع الكبير ذو الضلع a+b ومجموع مساحات المثلثات الأربع. مساحة المربع الكبير هي ²(a+b) لأن طول ضلعه هو a+b. ومجموع مساحات المثلثات هي أربع مرات مساحة مثلث واحد، أي 4(ab/2)، إذن الفرق هو (a+b)²-4(ab/2) بالتبسيط a²+b²+2ab-2ab أي a²+b². بهذا نكون قد برهنا على أن مساحة المربع ذو الضلع c تساوي a²+b²، أي a²+b²=c².

توجد طرق عديدة أخرى لإثبات مبرهنة فيثاغورس، حتى الرئيس الأمريكي الواحد والعشرون جيمس جارفيلد، برهن بطريقة قريبة من الطريقة السابقة، على مبرهنة فيثاغورس.