Зміст

1. Теоретичні відомості……………………………………….3 – 10

2. Приклади розв’язування типових завдань…….11 – 16

3. Тести………………………………………………………………….17

4. Підготовка до НМТ з математики…………………….18

5.Відео…………………………………………………………………..19 – 22

6. Завдання для самостійної роботи…………………..23 – 26

Теоретичні відомості

Означення: Функція F(x) називається первісною для функції f(x) на заданому проміжку, якщо для всіх  з цього проміжку виконується рівність: F′(x) = f(x)

Операція зна­ходження первісних для даної функції називається інтегруван­ням.

Основна властивість первісної:

Якщо функція F (x) є первісною для функції f (x) на даному проміжку, а C — довільна стала, то функціяF (x) + C також є первісною для функції f (x), при цьому будь-яка первісна для функції f (x) на даному проміжку може бути записана у вигляді F (x) + C, де C — довільна стала.

Геометрично основна властивість первісної означає, що графіки будь – яких первісних для даної функції одержуються один з одного паралельним перенесенням уздовж осі Oy.

Означення: інтегра́л  — одне із найважливіших понять математичного аналізу, яке виникає при вирішенні завдань:

– знаходження площі під кривою;

– пройденого шляху при нерівномірному русі;

– маси неоднорідного тіла, і тому подібних.

Означення: ви́значений інтегра́л — в математичному аналізі це інтеграл функції з вказаною областю інтегрування.

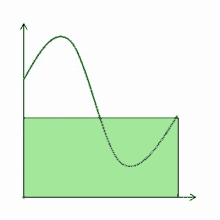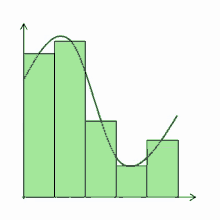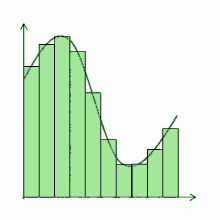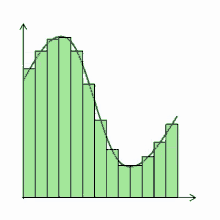
Означення: криволінійна трапеція — фігура на площині, обмежена графіком невід’ємної неперервної функції , визначеною на відрізку [a; b], віссю абсцис і прямими та .

Для знаходження площі криволінійної трапеції користуються визначеним інтегралом:

Для обчислення визначеного інтегралу використовують формулу Ньютона – Лейбніца:

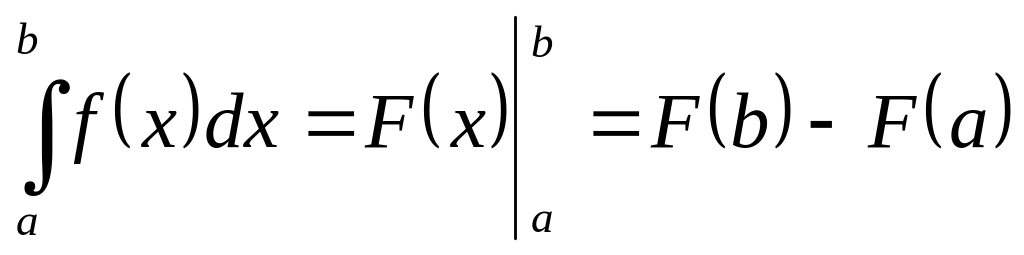
Приклади розв’язування типових завдань

Задача 1: Які з функцій є первісними для функції f(x) = – 2.

1) F(x)= 3х;

2) F(x)= – 3х + 1;

3) F(x)= – 2х;

4) F(x)= – 2х + 7.

Розв′язання:

1) і 2) – не є первісними;

3) і 4) – є первісними для даної функції, оскільки

F′(x) = (- 2х)′ = – 2,

F′(x) = (- 2х + 7)′ = – 2.

Відповідь: 3) і 4)

Задача 2: Чи є функція  первісною для функції , якщо:

F(x) = х³ – 3х² + 9х + С, 

f(x) = 3х² – 6х, х є R

Розв′язання:

F ′ (x) = 3х² – 6х + 9

Тому функція F(x) не є первісною для f(x).

Відповідь: не є.

Задача 3: Користуючись таблицею первісних та правилами знаходження первісних обчисліть первісну для функцій:

1) f (x) = 10x⁹

2) f (x) = 14x⁶

Розв′язання:

1) F(x) = 10 ·  x¹⁰ = x¹⁰ + С

2) F(x) = 14 · x⁷ = 2x⁷ + С                                      

Задача 4: Для даної функції  f (x) знайдіть первісну, графік якої проходить через точку А( 2; – 2).

f (x) = 9х² – 2х

Розв′язання:

F(x) = 9 ·  х³ – 2 ·  х² = 3х³ – х² + С

Знаючи, що графік проходить через точку А( 2; – 2), запишемо:

-2 = 3·2³ – 2²  + С

С = -2 – 24 + 4

С = – 22

Тому F(x) = 3х³ – х² – 22

Відповідь: F(x) = 3х³ – х² – 22

Тести

1. Виконайте тести за посиланням:

https://vseosvita.ua/test/start/sgu833

2. Виконайте інтерактивну вправу:

Підготовка до НМТ з математики

Виконайте завдання за посиланням:

https://zno.osvita.ua/mathematics/tag-pervisna_ta_viznachenij_integral/

Відео

Перегляньте навчальне відео: