
Тіла обертання

by Tetyana Masych
Artwork: Тетяна Масич
- Joined Jun 2023
- Published Books 20
Copyright © 2023

Зміст
1. Теоретичні відомості……………………………………….3 – 10
2. Приклади розв’язування типових завдань…….11 – 20
3. Тести………………………………………………………………….21
4. Підготовка до НМТ з математики…………………….22
5.Відео…………………………………………………………………..23 – 25
6. Завдання для самостійної роботи…………………..26 – 30

Теоретичні відомості
Циліндр
Означення: циліндр — це тіло обертання, отримане при обертанні прямокутника навколо його сторони.
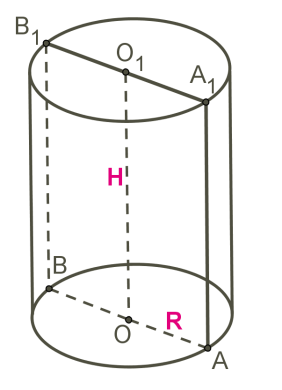
Прямокутник AOO1A1 обертається навколо сторони OO1.
OO1 — вісь циліндра і висота циліндра.
AA1 — твірна циліндра, довжина якої дорівнює довжині висоти циліндра.
Кола з центрами О та O1 — основи циліндра.
AO — радіус циліндра.
Означення: твірні циліндра — відрізки, що сполучають відповідні точки кіл основ циліндра.
Означення: осьовий переріз циліндра — це перетин циліндра площиною, яка проходить через вісь циліндра. Цей переріз є прямокутником.
При перерізі циліндра площиною, паралельною осі циліндра (тобто перпендикулярною основі), також виходить прямокутник.
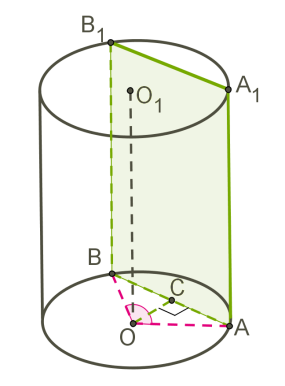
На малюнку зображений циліндр, перетнутий площиною, яка паралельна осі циліндра OO1.
ABB1A1 — прямокутник.
OA = ОB = R — радіуси.
OC — відстань від осі циліндра до площини перерізу.
При перерізі циліндра площиною, паралельною основі, в перерізі отримуємо коло, що дорівнює основам циліндра.
Якщо уявити, що бічна поверхня циліндра розрізана по твірній і розгорнута, то отримаємо прямокутник.
Оскільки розгортка — прямокутник, тоді площа бічної поверхні визначається за формулою:
Sбіч = 2πR ⋅ H
Основи циліндра — два круги із загальною площею 2⋅πR2
Площа повної поверхні циліндра визначається за формулою:
Sпов = 2πRH+2πR2=2πR ⋅ (H+R)
Об’єм циліндра визначається за формулою:
V = πR2 ⋅ H

Конус
Означення: конус — тіло обертання, утворене в результаті обертання прямокутного трикутника навколо його катета.
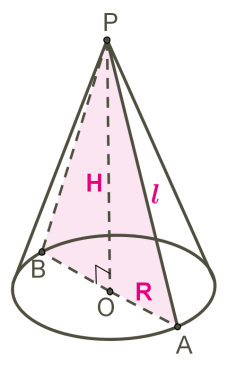
Трикутник POA обертається навколо сторони PO.
PO — вісь конуса і висота конуса.
P — вершина конуса.
PA — твірна конуса.
Коло з центром O — основа конуса.
AO — радіус основи конуса.
Означення: відрізок, що сполучає вершину конуса з точкою кола його основи називається твірною конуса.
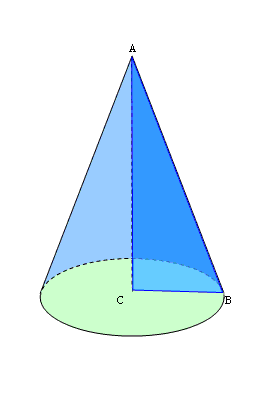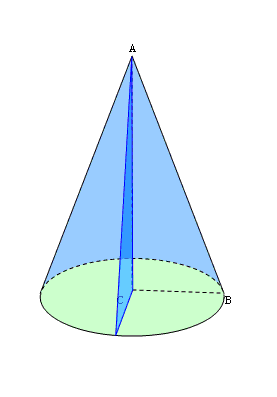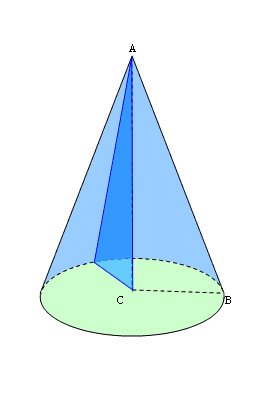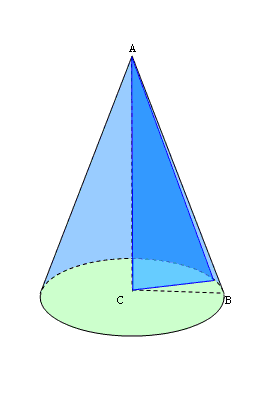
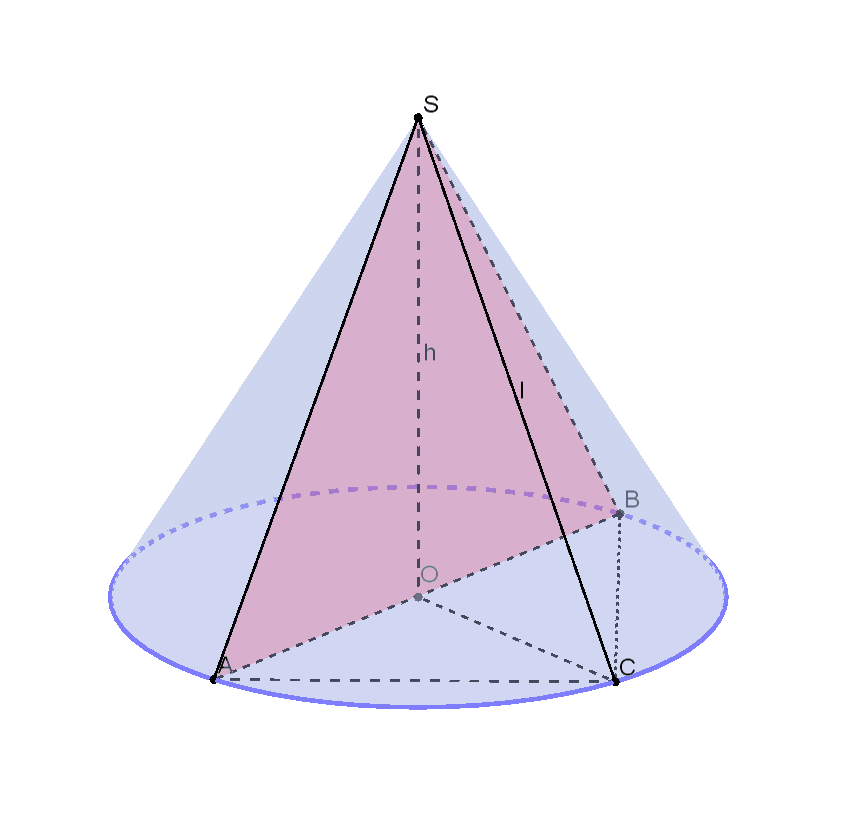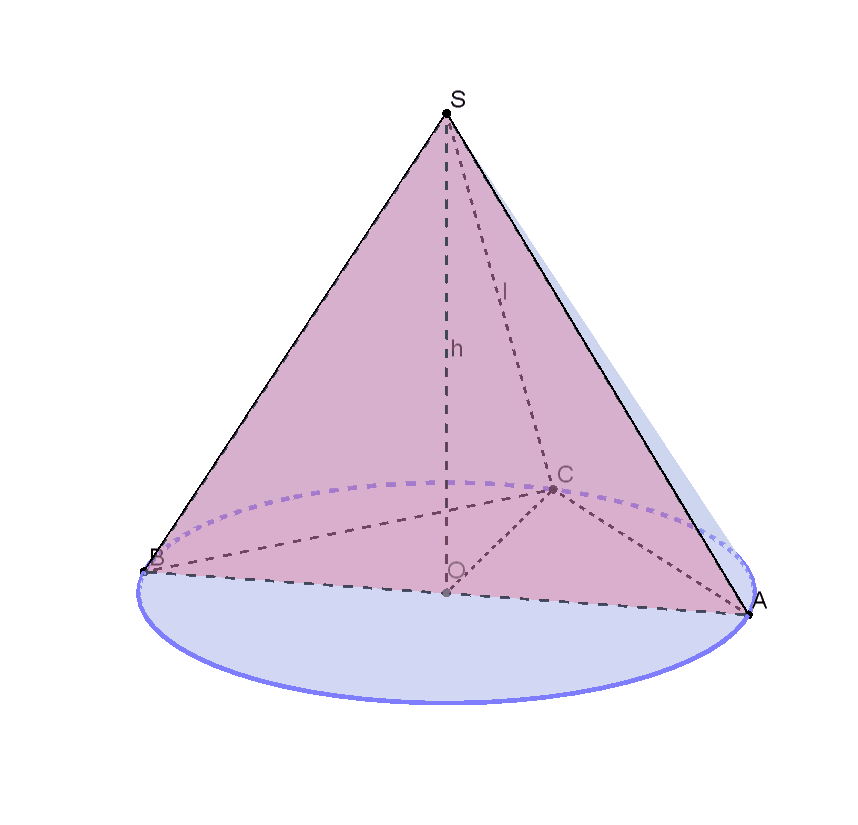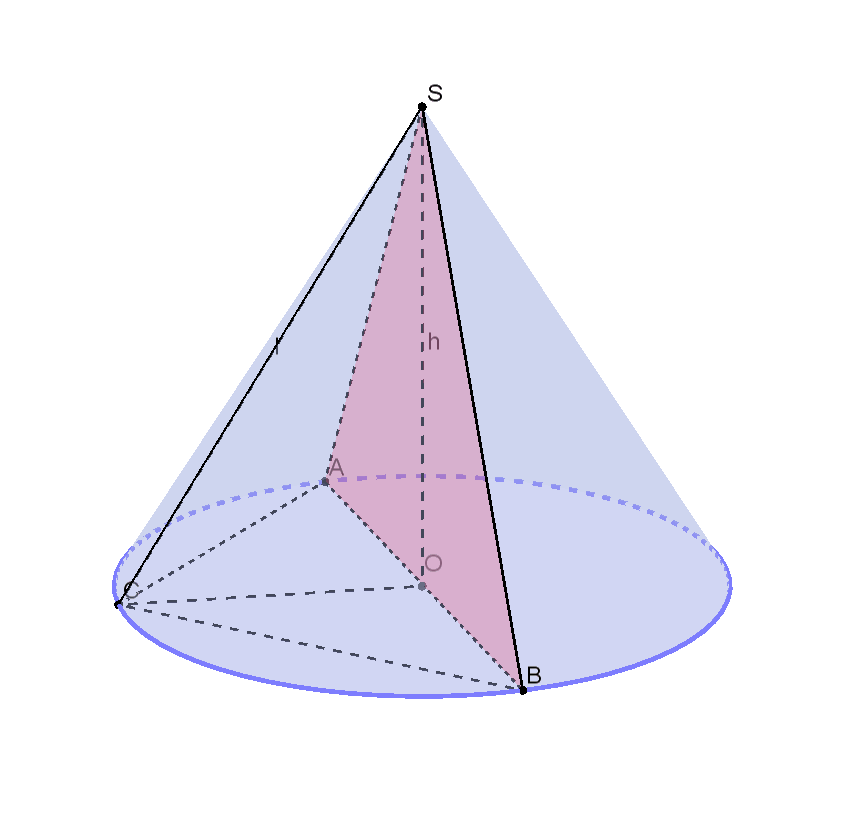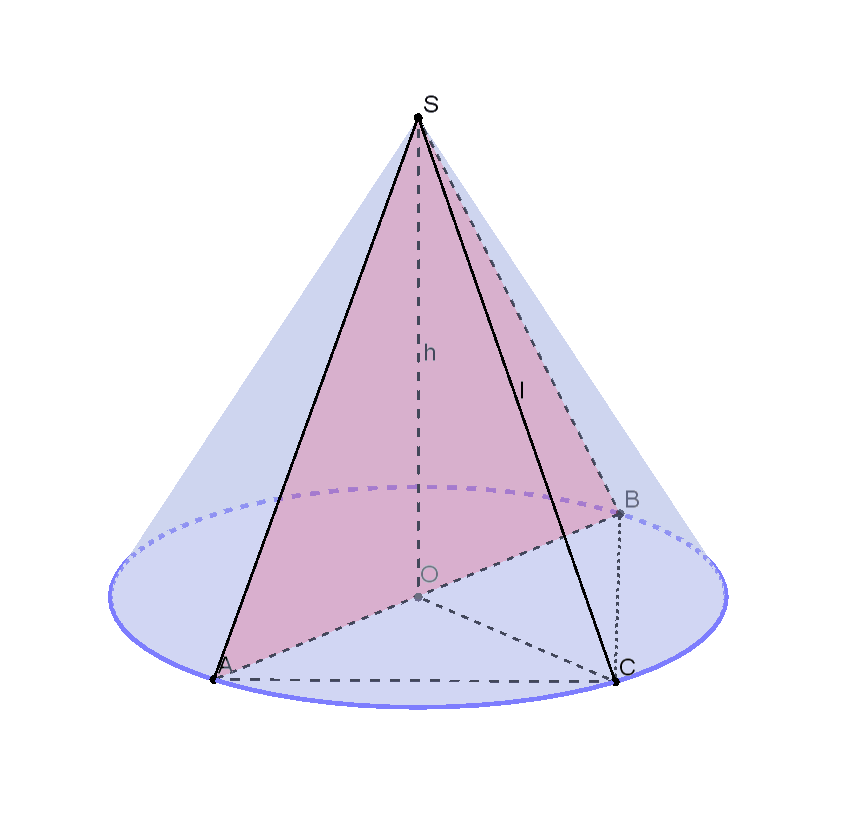
Означення: осьовий переріз конуса — це переріз конуса площиною, яка проходить через вісь PO конуса.
Осьовий переріз конуса — це трикутник.

ASB — осьовий переріз конуса.
∡SAO=∡SBO — кути між твірними і основою конуса.
При перерізі конуса площиною, паралельною осі конуса (тобто перпендикулярною основі), також виходить трикутник.
При перерізі конуса площиною, паралельною основі, в перерізі отримуємо коло.
Розгорткою бічної поверхні конуса є круговий сектор. Довжина дуги сектора — це довжина кола основи конуса довжиною 2πR. Радіус сектора — це твірна конуса.
Площа бічної поверхні конуса визначається за формулою:
Sбіч. = πRℓ, де ℓ – твірна
Площа повної поверхні конуса визначається за формулою:
Sп= πRℓ + πR2=πR(ℓ+R)
Об’єм конуса обчислюються за формулою:
V = ⅓πR2 ⋅ H
Куля
Означення: куля — це тіло обертання, отримане при обертанні півкруга навколо осі, що містить його діаметр.
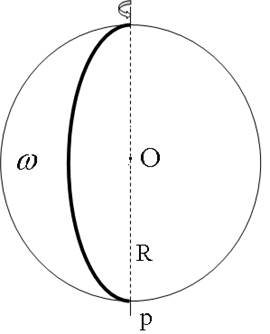
Точка О — центр кулі.
ОР — радіус кулі.
Усякий переріз кулі площиною є круг.
Означення: якщо переріз проходить через діаметр кулі, то її називають діаметральною площиною.
Означення: переріз кулі діаметральною площиною називають великим кругом.
Об’єм кулі обчислюється за формулою:
V = ⁴/₃πR3, де R — радіус кулі.
Сфера
Означення: поверхню кулі називають сферою.

Точка О — центр сфери.
ОС — радіус, АВ — діаметр сфери.
Означення: переріз сфери діаметральною площиною називають великим колом.
Площа сфери обчислюється за формулою:
S = 4πR2 , де R — радіус сфери.

Приклади розв’язування типових завдань
Задача 1: Площа повної поверхні циліндра дорівнює 92π, а площа його бічної поверхні — 56π. Визначте площу основи цього циліндра.
Розв’язання:
З формули Sп=Sб+2Sосн
2Sосн = Sп – Sб = 92π – 56π = 36π
Тоді Sосн = 36π:2 = 18π
Відповідь: Sосн = 18π

Задача 2: Циліндр, радіус основи якого дорівнює 4 см, висота — 12 см, перетнули площиною, паралельною до його основи. Утворилося два циліндри. Визначте суму площ повних поверхонь утворених циліндрів.
Розв’язання:
Площа бічної поверхні циліндра до розрізання дорівнює
S = 2πRH = 2π ⋅ 4 ⋅ 12 = 96π см2.
Після розрізання маємо два циліндри, сума площ бічних поверхонь яких дорівнює площі бічної поверхні початкового циліндра. Дані циліндри мають однакові основи. Площа однієї з них S = πR2 = 16π см2.
Разом маємо чотири основи.
Тоді сума площ повних поверхонь буде дорівнювати
96π + 4⋅16π = 160π см2
Відповідь: 160π см2
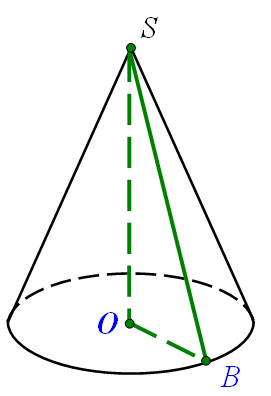
Задача 3: Твірна конуса дорівнює 2 см і нахилена до площини основи під кутом α. Знайдіть: а) висоту конуса;
б) радіус основи; в) площу осьового перерізу.
Розв’язання:
SB = 2 см; ∠ ABO = α
а) SО = SB · cos α = 2cos α;
б) ОВ = SB · sin α = 2sin α;
в) Sо.п. = 2SSOB = 2 · ⅟₂ · SB · cos α · SB · sin α =
= 4 · cos α · sin α = 2sin 2α
Відповідь: а) 2cos α; б) 2sin α; в) 2sin 2α


Задача 4: Прямокутний трикутник, гіпотенуза якого дорівнює 8 см, а один із кутів дорівнює 30°, обертається навколо більшого катета. Знайдіть площу бічної поверхні утвореного конуса.
Розв’язання:
ВС = 8 см; ∠ АВС = 30°; ∠ А = 90°
Більший катет АВ – висота конуса, менший катет АС – радіус конуса, гіпотенуза – твірна конуса.
Скористаємося властивістю про катет прямокутного трикутника, який лежить проти кута 30° і дорівнює половині гіпотенузи.
АС = ⅟₂ · BС = ⅟₂ · 8 = 4 см
Sбіч. = πRℓ = π · 4 · 8 = 32π см2
Відповідь: 32π см2

Задача 5: Кулю, радіус якої 5см, перетнуто площиною, що розміщена на відстані 3 см від центра. Знайти площу перерізу.
Розв’язання:
ОО1=3 см, ОА=5см.
О1А2 = 52 – 32 = 25 – 9 = 16
О1А = 4 см
S = πR2 = 16π см2
Відповідь: 16π см2
Задача 6: М’яч, площа поверхні якого дорівнює
400π см2 зробив один повний оберт по прямій. Знайти довжину шляху, яку він при цьому подолав.
Розв’язання:
Оскільки площа сфери S = 4πR2
Тоді 400π = 4πR2
R2 = 100
R=10 см
Довжина шляху S = 2πR = 2π · 10 = 20π cм
Відповідь: 20π cм

Тести
1. Виконайте тести за посиланням:
https://vseosvita.ua/test/start/zyj384
2. Виконайте тести за посиланням:
https://vseosvita.ua/test/start/nvb754
3. Виконайте інтерактивну вправу:
Підготовка до НМТ з математики
Виконайте завдання за посиланням:
https://zno.osvita.ua/mathematics/tag-tila_obertannja/

Відео
Перегляньте навчальне відео:
Завдання для самостійної роботи




Published: Jul 11, 2023
Latest Revision: Jul 11, 2023
Ourboox Unique Identifier: OB-1476620
Copyright © 2023







