
Багатогранники

by Tetyana Masych
Artwork: Тетяна Масич
- Joined Jun 2023
- Published Books 20
Copyright © 2023

Зміст
1. Теоретичні відомості……………………………………….3 – 14
2. Приклади розв’язування типових завдань…….15 – 24
3. Тести………………………………………………………………….25
4. Підготовка до НМТ з математики…………………….26
5.Відео…………………………………………………………………..27 – 30
6. Завдання для самостійної роботи…………………..31 – 32

Теоретичні відомості
Багатогранник та його елементи
Означення: багатогранником називають тіло (частина простору), обмежене скінченою кількістю плоских багатокутників.
Багатокутники, які обмежують багатогранник, називають його гранями, їх сторони — ребрами, а вершини — вершинами багатогранника.
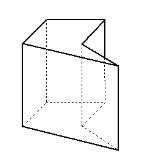
Опуклий багатогранник Неопуклий багатогранник
Призма
Означення: призма — це багатогранник, дві грані якого є рівними багатокутниками, що знаходяться в паралельних площинах, а інші грані — паралелограми.
Грані, які знаходяться в паралельних площинах, називаються основами призми, а інші грані — бічними гранями призми.
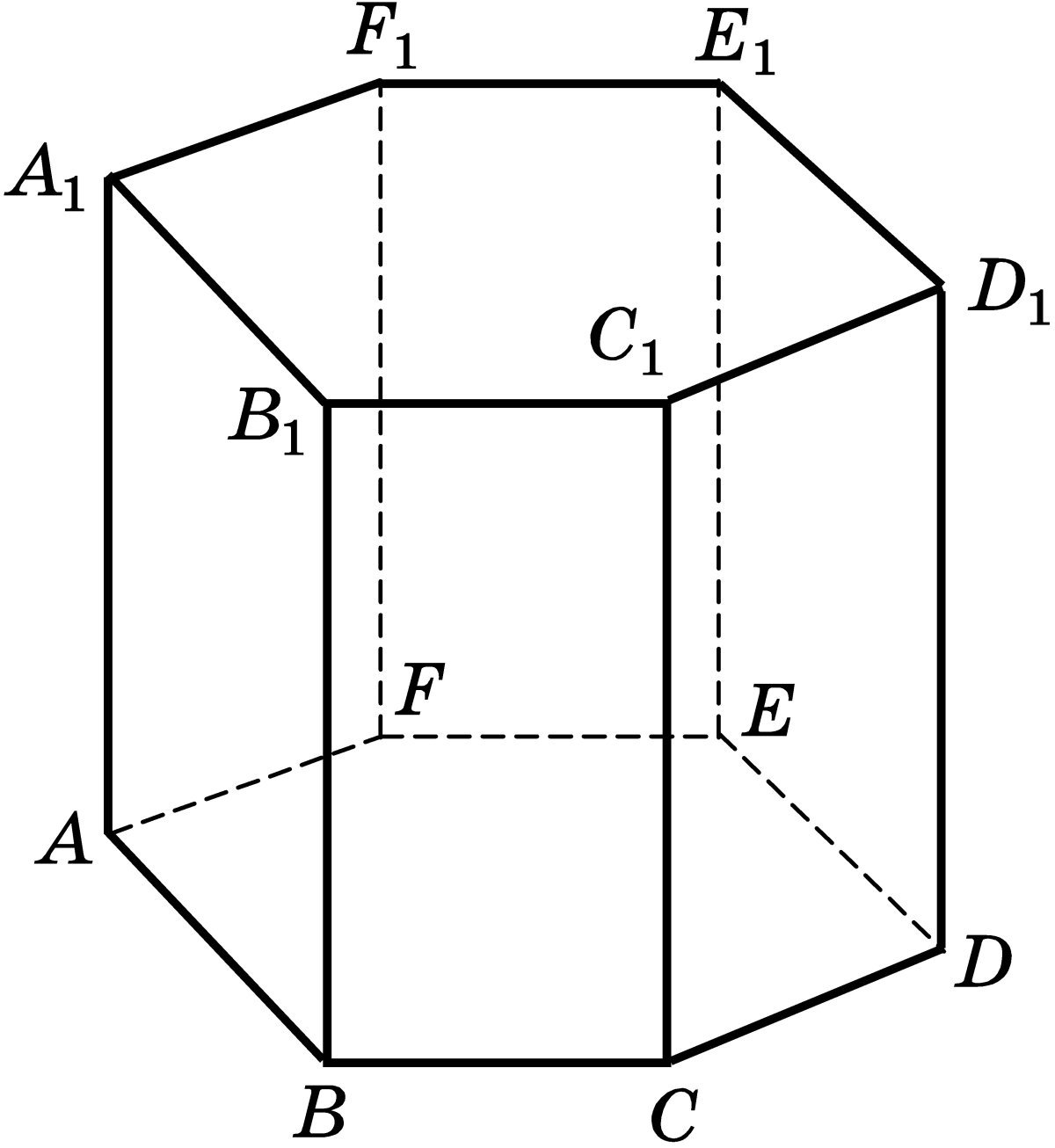
Залежно від основи призми бувають: трикутними, чотирикутними, шестикутними і т.д.
Означення: призма з бічними ребрами, перпендикулярними її основам, називається прямою призмою.
Означення: пряма призма називається правильною, якщо її основи — правильні багатокутники.
Означення: відстань між основами призми називається висотою призми.
![]() Висота прямої призми збігається з бічним ребром.
Висота прямої призми збігається з бічним ребром.![]()
Означення: площею бічної поверхні (бічною поверхнею) призми називається сума площ бічних граней.
Бічна поверхня прямої призми дорівнює добутку периметра основи на висоту призми, тобто на довжину бічного ребра.
Sбіч = Росн · H
Означення: площа повної поверхні дорівнює сумі бічної і двох площ основи.
Sпов = Sбіч + 2Sосн
Означення: Об′єм прямої призми дорівнює добутку площі її основи на висоту.
V = Sосн · H

Паралелепіпед
Означення: Паралелепіпед — це чотирикутна призма, основою якої є паралелограмам.
Властивості паралелепіпеда
1. Протилежні грані паралелепіпеда паралельні та рівні.
2. Діагоналі паралелепіпеда перетинаються і точкою перетину діляться навпіл.

Означення: Прямий паралелепіпед, у якого основою є прямокутник, називається прямокутним паралелепіпедом.
Властивості прямокутного паралелепіпеда
1. Квадрат діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів його лінійних розмірів.
2. Усі чотири діагоналі прямокутного паралелепіпеда рівні.
Означення: Прямокутний паралелепіпед, всі лінійні розміри якого рівні, називається кубом.
Площа повної поверхні куба обчислюється за формулою:
Sпов = 6а2
Об′єм прямокутного паралелепіпеда обчислюється за формулою: V = а · b · c
Об′єм куба обчислюється за формулою: V = а3

Піраміда
Означення: пірамідою називається багатогранник, одна грань якого – довільний багатокутник, а решта трикутники, що мають спільну вершину.
Означення: висотою піраміди називають перпендикуляр, опущений з її вершини на площину основи.
Означення: висоту бічної грані правильної піраміди називають апофемою.
Означення: піраміда називається правильною, якщо її основа – правильний багатокутник, центр якого збігається з основою висоти піраміди.
Означення: піраміда називається правильною, якщо її основа – правильний багатокутник, центр якого збігається з основою висоти піраміди.
Означення: площа бічної поверхні правильної піраміди дорівнює добутку півпериметра основи на апофему.
Sбіч = 1/2 · Росн · H, де H – апофема
Означення: площа повної поверхні правильної піраміди дорівнює сумі площ бічної поверхні та основи піраміди.
Sпов = Sбіч + Sосн
Означення: Об′єм піраміди дорівнює третині добутку площі її основи на висоту.
V = 1/3 · Sосн · H

Правильні багатогранники
Означення: правильним багатогранником називають опуклий багатогранник, у якого всі грані — рівні правильні багатокутники й у кожній вершині сходиться однакове число ребер.
Всього існує 5 видів правильних багатогранників: тетраедр, гексаедр, октаедр, додекаедр, ікосаедр.
Означення: правильний тетраедр — складається з чотирьох правильних трикутників, в кожній вершині сходиться по 3 ребра. Отже, сума плоских кутів при кожній вершині дорівнює 3·60° = 180° < 360°. Він має 4 грані, 4 вершини і 6 ребер.
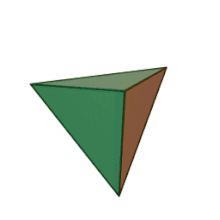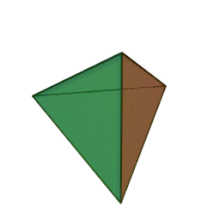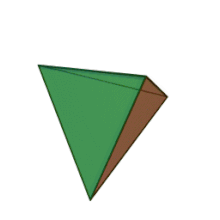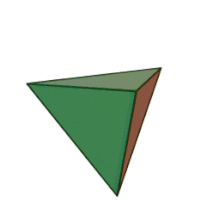
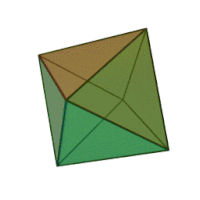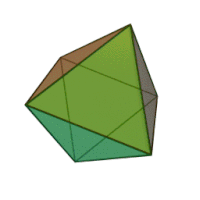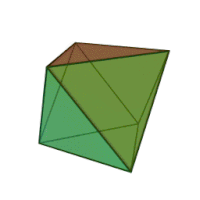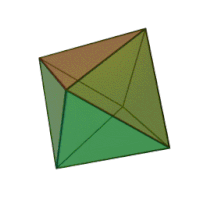
Означення: октаедр — це багатогранник, поверхня якого складається з восьми правильних трикутників і в кожній вершині сходиться по чотири ребра. Отже, сума плоских кутів при кожній вершині дорівнює 4·60° = 240° < 360°. Він має 8 граней, 8 вершин і 12 ребер.
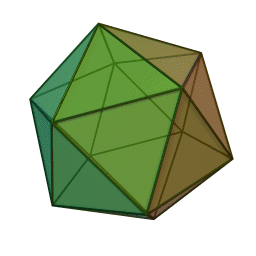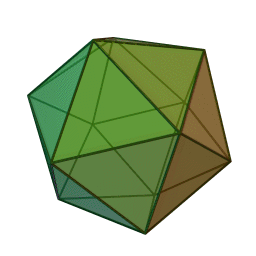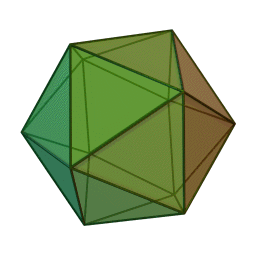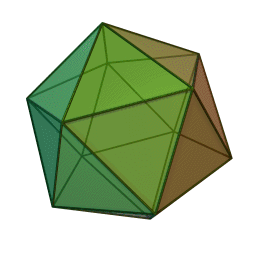
Означення: ікосаедр — це багатогранник, поверхня якого складається з двадцяти правильних трикутників і в кожній вершині сходиться по п’ять ребер. Отже, сума плоских кутів при кожній вершині дорівнює 5·60° = 300° < 360°. Він має 20 граней, 12 вершин і 30 ребер.
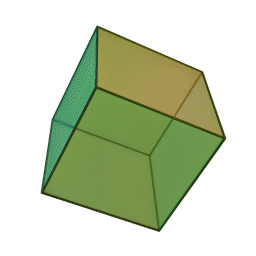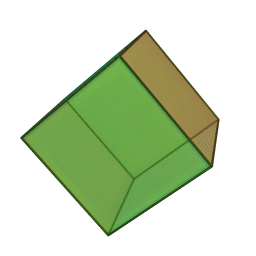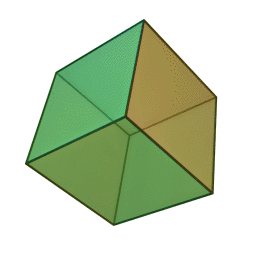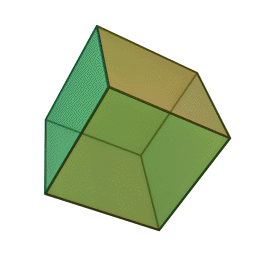
Означення: гексаедр — це багатогранник, поверхня якого складається із шести квадратів і в кожній вершині сходиться по три ребра. Отже, сума плоских кутів при кожній вершині дорівнює 3·90° = 270° < 360°. Він має 6 граней, 8 вершин і 12 ребер.
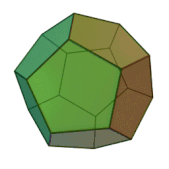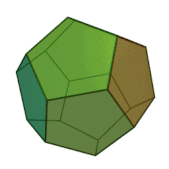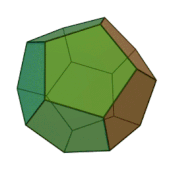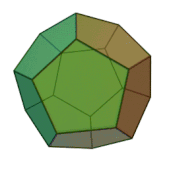
Означення: додекаедр — це багатогранник, поверхня якого складається з дванадцяти правильних п’ятикутників і в кожній вершині сходиться по 3 ребра. Отже, сума плоских кутів при кожній вершині дорівнює 3·108° = 324° < 360°. Він має 12 граней, 20 вершин і 30 ребер.

Приклади розв’язування типових завдань
Задача 1: На фабриці випускають шоколадні цукерки у вигляді прямої призми, в основі якої лежить ромб з діагоналями 24 см и 10 см. Площа повної поверхні призми дорівнює 500 см2. Яка буде висота цієї коробки?
Розв’язання:
Sпов = Sбіч + 2Sосн
Sосн = ½ · d1 · d2 = ½ · 24 · 10 = 120 см2
2Sосн = 2 · 120 = 240 см2
Sбіч = Росн · H
Діагоналі ромба в точці перетину діляться навпіл.
Тому, сторону ромба знайдемо за т. Піфагора:
а2 = 122 + 52 = 144 + 25 = 169
а = 13 см
Росн = 4а = 4 ·13= 52(см);
Підставимо у першу формулу:
500 = 240 + 52 · H;
52 H = 260;
H = 5 см.
Відповідь: 5 см
Задача 2: Куб з ребром 1 м поділили на кубики з ребром
1 см й усі ці кубики поставили в стовпець. Чому дорівнює висота стовпця? Чи перевищить висота стовпця висоту нашого ліцею?
Розв’язання:
V куба = 1м3 = 100 см · 100 см · 100 см = 1 000 000 см3
V кубика = 1 см3
кількість кубиків = V куба : V кубика = 1 000 000(шт.) – кубиків об’ємом 1 см3
H =1 000 000 см = 10 км
Відповідь: 10 км; так, перевищить.


Задача 3: Знайти діагональ прямокутного паралелепіпеда, виміри якого дорівнюють 2 см, 3 см і 6 см.
Розв’язання: Всі грані прямокутного паралелепіпеда є прямокутники.
Нехай довжини ребер паралелепіпеда дорівнюють a=2 см, b=3 см і c=6 см.
Тоді діагональ DB1 = d прямокутного паралелепіпеда обчислюють за формулою:
d2 = а2 + b2 + с2 = 22 + 32 + 62 = 4 + 9 + 36 = 49
d = 7 см.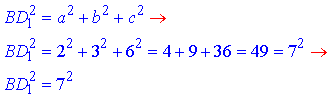
Відповідь: 7 см

Задача 4: Основою піраміди є прямокутник зі сторонами
6 см і 15 см. Висота піраміди дорівнює 4 см і проходить через точку перетину діагоналей основи. Знайдіть площу бічної поверхні піраміди.
Розв’язання:
АВ = 6 см, АD = 15 см, SO = 4 см.
ОN = ½ АD = 7,5 см; ОМ = ½ АВ = 3 см.
SN2 = 16 + 56,25 = 72,25
SN = 8,5 см
SМ2 = 16 + 9 = 25
SМ = 5 см
Sбіч = 2SCSD + 2SASD = СD · SN + AD · SM = 6·8,5 + 15·5 =
= 51 + 75 = 126 см2
Відповідь : 126 см2
Підготовка до НМТ з математики
Задача 5: Сторона основи правильної чотирикутної піраміди дорівнює 4 см, а об’єм — 64 см3. Знайдіть висоту піраміди.
| А | Б | В | Г | Д |
| см | 4 см | 8 см | 12 см | 16 м |
Розв’язання:
Оскільки піраміда правильна чотирикутна, то в основі лежить квадрат. Тоді площа основи S=42=16. Об’єм піраміди знаходимо за формулою V=Sоснh:3. Маємо 64=16⋅h:3. Звідси h=64:16⋅3=12 см.
Відповідь: Г.
Задача 6: Визначте довжину апофеми правильної чотирикутної піраміди, якщо площа її повної поверхні дорівнює 208 см2, а довжина сторони основи — 8 см.
| А | Б | В | Г | Д |
| 13 см | 12 см | 9 см | 8 см | 6 см |
Розв’язання:
Так як піраміда правильна чотирикутна, то в основі лежить квадрат. Тоді площа основи піраміди Sосн=a2=82=64 см2. Площа повної поверхні правильної піраміди Sповна=Sбічна+Sосн, звідки Sбічна=Sповна-Sосн=208-64=144 см2. Периметр основи (квадрата) дорівнює 4a=4⋅8=32 см. Площа бічної поверхні правильної піраміди дорівнює половині добутку периметра основи на апофему, тому маємо 144=32⋅ha:2, звідки довжина апофеми ha=144:32⋅2=9 см.
Відповідь: В.
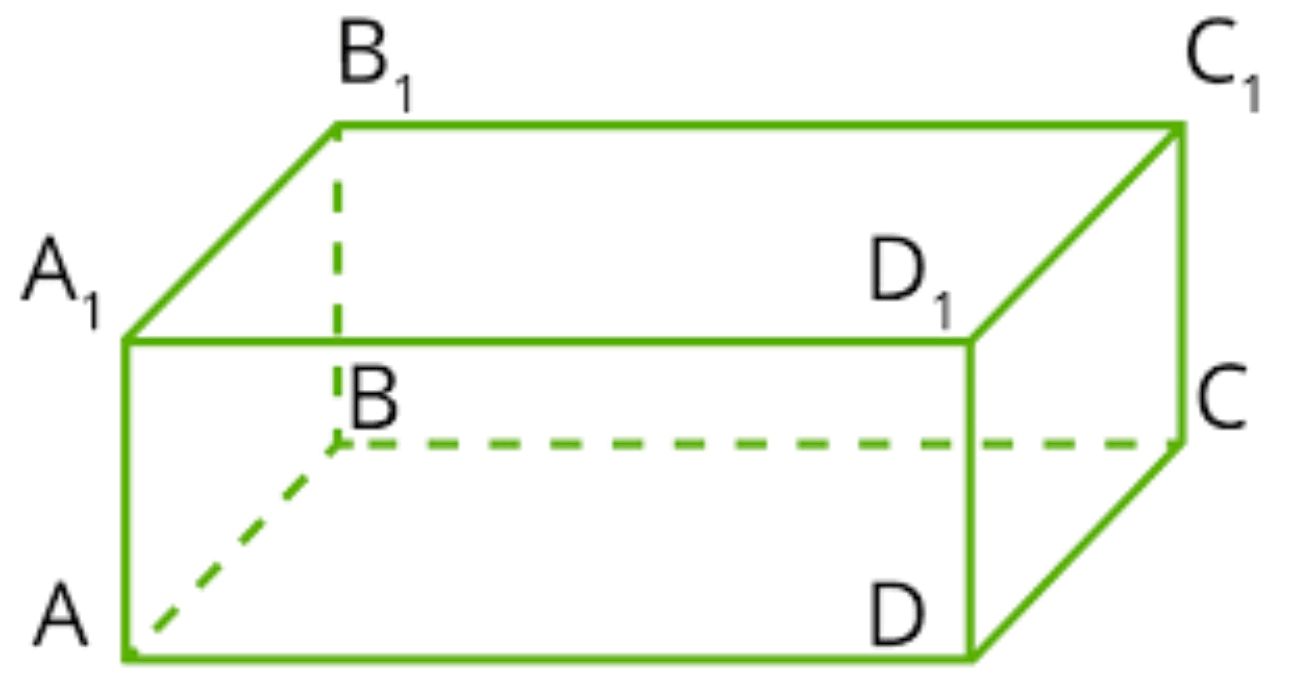
Задача 7: На рисунку зображено прямокутний паралелепіпед ABCDA1B1C1D1, у якому АВ = 3, AD = 4, AA1=2. Увідповідніть початок речення (1-3) так, щоб утворилося правильне речення.
| Початок речення | Закінчення речення |
| 1 Відстань від точки С до площини (АA1В1) дорівнює 2 Відстань від точки А до прямої СC1 дорівнює 3 Відстань між площинами (АВС) і (A1B1C1) дорівнює |
А 2 Б 3 В 4 Г 5 Д 7 |
Розв’язання:
1) Відстанню від точки С до площини (АA1В1) є відрізок СВ, який дорівнює АD і дорівнює 4.
2) Відстанню від точки А до прямої СC1 є відрізок АС, який з прямокутного трикутника ADC можна знайти за теоремою Піфагора (використовуючи “єгипетський” трикутник одразу маємо АС=5).
3) Відстанню між площинами (АВС) і (A1B1C1) є відрізок AA1=2.
Відповідь: 1-В, 2-Г, 3-А.
Тести
1. Виконайте тести за посиланням:
https://vseosvita.ua/test/start/hpp634
2. Виконайте інтерактивну вправу:
Підготовка до НМТ з математики
Виконайте завдання за посиланням:
призма:
https://zno.osvita.ua/mathematics/tag-mnogogranniki/
піраміда:
https://zno.osvita.ua/mathematics/tag-piramida/

Відео
Перегляньте навчальне відео:
Завдання для самостійної роботи
Інтерактивна вправа «Закінчи речення»
1. Тіла, поверхні яких складаються зі скінченної кількості плоских багатокутників називаються…
2. Багатогранник, який складається з плоского багатокутника та точки, яка не лежить у його площині і всіх відрізків, що сполучають цю точку з точками плоского багатокутника називається…
3. Точка, яка не лежить у площині основи піраміди називається…
4. Відрізки, що сполучають вершину піраміди з вершинами основи, називаються…
5. Фігура, яка є бічною гранню піраміди це…
6. Перпендикуляр, опущений з вершини піраміди на площину основи називається…
7. Суму площ усіх бічних граней піраміди називають…
8. Кількість граней куба дорівнює…
9. Багатокутник називається правильним, якщо…
10. Центром правильного багатокутника називають…
11. Правильних багатогранників існує…
12. Усі бічні ребра правильної піраміди…
13. Усі грані прямокутного паралелепіпеда…
14. Кількість ребер прямокутного паралелепіпеда дорівнює…
15. Апофема – це…
16. Які із зображених на малюнку тіл є багатогранниками?


Published: Jul 7, 2023
Latest Revision: Jul 7, 2023
Ourboox Unique Identifier: OB-1475370
Copyright © 2023








