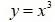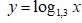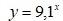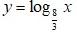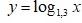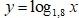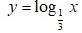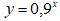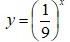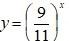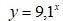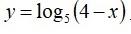Зміст

1. Теоретичні відомості……………………………………….3 – 9

2. Приклади розв’язування типових завдань…….10 – 16

3. Тести………………………………………………………………….17

4. Підготовка до НМТ з математики…………………….18

5.Відео…………………………………………………………………..19 – 22

6. Завдання для самостійної роботи…………………..23 – 26

Теоретичні відомості

Показникова функція

Означення: Функція задана формулою у=а^х, де а>0 і а ≠ 1 називається показниковою.

Наприклад:  у=2^х, у=7^х, у=(1/2)^х, у=π^х – показникові функції.

Графік показникової функції

Графіком показникової функції є крива, яка називається експонентою.

при а > 1                                            при 0 < а < 1

Розглянемо властивості показникової функції:

Логарифмічна функція

Логарифми та їх властивості

Означення: Логарифмом числа b за основою а називається показник степеня до якого треба піднести основу а, щоб отримати b.

Вираз log_ab має зміст, якщо а > 0, а ≠ 1 і b > 0.

Означення: Логарифм числа b за основою 10 називають десятковим і позначають lg b.

Означення: Логарифм числа b за основою е називають натуральним і позначають ln b.

Означення: Функцію, задану формулою у = log_aх (а > 0, 

а ≠ 1) називають логарифмічною функцією.

Графік логарифмічної функції

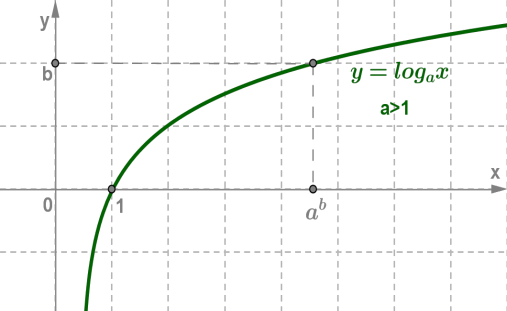
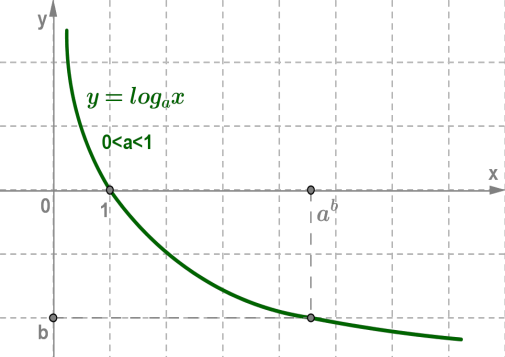
при а > 1                                   при 0 < а < 1

Розглянемо властивості логарифмічної функції:

Правило: log_ab > 0, якщо а і b розташовані по один бік від 1, тобто а > 1, b > 1 або 0 < а < 1, 0 < b < 1.

log_ab < 0, якщо а і b розташовані по різні боки від 1, тобто 0 < а < 1, b > 1 або а > 1, 0 < b < 1.

Використовуючи це правило можна порівнювати логарифми з нулем та між собою.

Приклади розв’язування типових завдань

Задача 1: Які з наведених функцій є показниковими:

1) у = 3^х;     2) у = х²;      3) у = 1^х;

4) у = (-4)^х;   5) у = х²⁰;    6) у = х^-10;

7) у = (2/3)^х;     8) у = (2 – х)⁵

Розв’язання:

За означенням показниковою є функція, яка задана формулою у=а^х, де а>0 і а ≠ 1.

Тому, 1) – показникова функція; 2) – ні;  3) – ні(бо а = 1);

4) – ні(бо а – від’ємне число);  5) – ні;   6) – ні;   7) – так;

8) – ні.

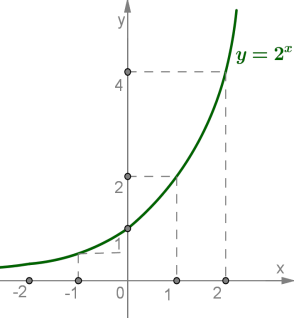
Задача 4: Побудуйте графік функції у =  2^х

Розв’язання:

Складемо таблицю значень функції:

Побудуємо на координатній площині точки з таблиці і з’єднає­мо ці точки плавною лінією. Одержимо графік функції у = 2^х

Тести

1. Виконайте тести за посиланням:

https://vseosvita.ua/test/start/asf807

2. Виконайте інтерактивну вправу:

Підготовка до НМТ з математики

Виконайте завдання за посиланням:

https://zno.osvita.ua/mathematics/tag-pokaznykovi_logharyfmichni_vyrazy/

Відео

Перегляньте навчальне відео:

Завдання для самостійної роботи

1. Яка з наведених функцій є показниковою?

2. Серед даних функцій вкажіть спадну

3. Серед даних функцій вкажіть зростаючу

4. Вкажіть координати точки, через яку проходить графік функції у =  5^х
(-1; -5);    (0; 1);    (0; 5);    (1; 0);    (-5; 0)

5. Знайдіть область визначення функції

x<2;    x>0;    x<4;    x<3;    x>4

6. Вкажіть область значень показникової функції:
– множина всіх дійсних чисел;
– множина всіх невід’ємних чисел;
– множина всіх додатних чисел, які не дорівнюють 1;
– множина всіх додатних чисел;
– множина всіх ненульових чисел

7. Вкажіть область визначення логарифмічної функції:
– множина всіх дійсних чисел;
– множина всіх невід’ємних чисел;
– множина всіх додатних чисел, які не дорівнюють 1;
– множина всіх додатних чисел;
– множина всіх ненульових чисел

8. Показникова й логарифмічна функція за однією і тією ж основою…
– обернені;
– протилежні;
– зростаючі;
– спадні;
– не визначені

9. Вкажіть правильні твердження
– графік показникової функції проходить через точку (0; 1)
– графік логарифмічної функції симетричний відносно осі Ох
– графіки показникової та логарифмічної функції з однією і   

   тією ж основою симетричні відносно прямої у = х
– логарифмічна функція завжди невід’ємна
– показникова функція не має найбільшого значення

10. Обчисліть значення виразу log₃45+log₃900-log₃500