Зміст

1. Теоретичні відомості……………………………………3 – 10

1.1. Перпендикулярність прямих…………………….3 – 4

1.2. Перпендикулярність прямої і площини……5 – 7

1.3. Перпендикулярність площин…………………….8 – 10

2. Приклади розв’язування типових завдань….11 – 20

3. Тести………………………………………………………………21

4. Підготовка до НМТ з математики…………………22

5. Відео………………………………………………………………23 – 26

6. Завдання для самостійної роботи………………..27 – 28

Теоретичні відомості

Перпендикулярність прямих

Означення: Дві прямі називаються перпендикулярними, якщо кут між ними дорівнює 90°.

Так само як і в площині, в просторі перпендикулярні прямі a і b позначають a⊥b.

У просторі перпендикулярними називають не тільки прямі, що перетинаються, а й мимобіжні прямі, тому що ми говоримо про кут, який можуть утворити ці прямі, якщо їх розташувати в одній площині.

Теорема: Якщо пряма перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна і до другої прямої.

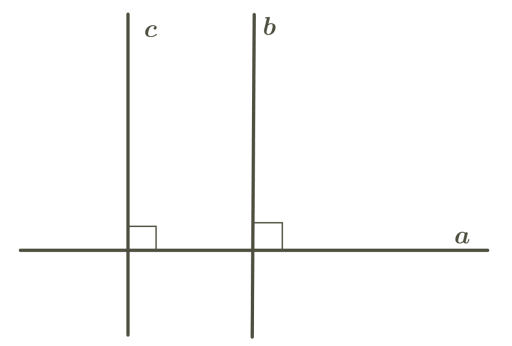
Означення: Кутом між мимобіжними прямими називається кут між прямими, які перетинаються і паралельні відповідно даним мимобіжним прямим.

Перпендикулярність прямої і площини

Означення: Пряма, що перетинає площину, називається перпендикулярною цій площині, якщо вона перпендикулярна кожній прямій, яка лежить у цій площині.

Ознака перпендикулярності прямої і площини:
Якщо пряма перпендикулярна до двох прямих, що перетинаються у площині, то вона перпендикулярна до площини.

Властивості перпендикулярності прямої і площини:

1. Дві прямі, перпендикулярні до однієї площини, паралельні.

2. Через дану точку проходить тільки одна площина, перпендикулярна до даної прямої.

Означення: Кутом між похилою і площиною називається кут між цією похилою і її проекцією на площину.

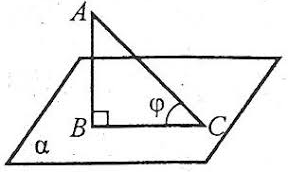
Теорема: Якщо з однієї точки, взятої поза площиною, проведено до цієї площини перпендикуляр і похилі, то:

1)проекції рівних похилих рівні;

2)із двох похилих більша та, проекція якої більша;

3)перпендикуляр коротший за будь – яку похилу.

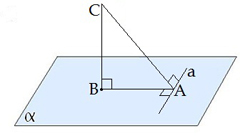
Теорема про три перпендикуляри

Теорема: Якщо пряма, проведена на площині через основу похилої, перпендикулярна її проекції, то вона перпендикулярна й самій похилій. і навпаки, Якщо пряма на площині перпендикулярна похилій, то вона перпендикулярна і проекції похилої.

Перпендикулярність площин

Означення: Двогранним кутом  називають  фігуру,  утворену двома півплощинами із спільною прямою, що їх обмежує.

Півплощини α і β, що утворюють двогранний кут, називаються його гранями.
Спільна пряма a цих граней називається ребром  двогранного кута.

Означення: Лінійним кутом двогранного кута називається кут, утворений в результаті перетину двогранного кута з площиною, яка перпендикулярна до ребра двогранного кута.

Означення: Дві площини, що перетинаються, називаються перпендикулярними, якщо будь-яка третя площина, перпендикулярна до прямої перетину цих площин, перетинає їх по перпендикулярних прямих.

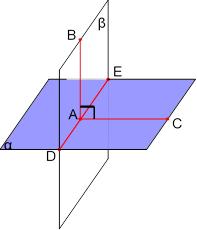
Ознака перпендикулярності площин: Якщо площина проходить через пряму, перпендикулярну до другої площини, то ці площини перпендикулярні.

Теорема: Якщо пряма, яка лежить в одній з двох перпендикулярних площин, перпендикулярна до лінії їх перетину, то вона перпендикулярна і до другої площини.

Якщо в просторі перетинаються дві площини, то утворюється чотири двогранних кути.

Величина двогранного кута  знаходиться в межах від 0° до 180°.

Якщо площини паралельні, то кут між ними дорівнює 0°.
Якщо площини перпендикулярні, то кут між ними дорівнює 90°

Приклади розв’язування типових завдань

Задача 1:

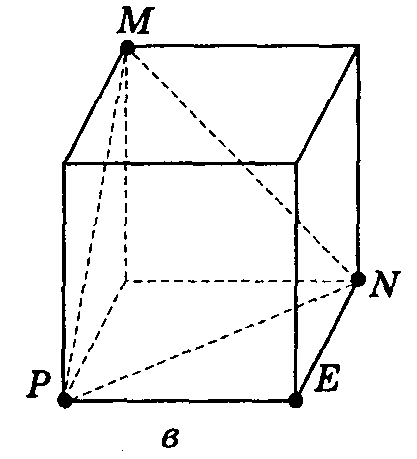
Дано: Куб, РЕ = 4 см

Знайти: Р_МNP

Розв’язання:

Всі грані куба є рівними квадратами. А отже і діагоналі цих квадратів будуть рівними. Тому трикутник MNP буде рівностороннім.

Із прямокутного трикутника PEN  PN = РЕ/ sin45° = 4 см.

Отже, Р_МNP = 3 · 4 = 12 см.

Задача 2:

Прямі AB, AC і AD попарно перпендикулярні. Знайдіть відрізок CD якщо: 1) AB =3 см, BC =7 см , AD = 1,5 см;

2) BD = 9 см , BC= 16 см , AD = 5 см;

3) AB =a, BC =b, AD = c.

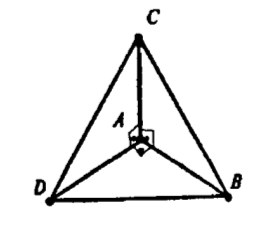
Дано: AB AC, AB AD, AC  AD

AB =3 см, BC =7 см , AD = 1,5 см ;

Знайти: CD

Розв’язання:

Трикутники САВ, САD і ВАD – прямокутні (за умовою).

З трикутника САВ  АС² = ВС² – АВ² = 49 – 9 = 40 см² 

(за т. Піфагора)

З трикутника САD  СD² = АС² + АD² = 40 + 2,25 =

= 42,25 см²   (за т. Піфагора)

СD = 6,5 см

Отже, СD = 6,5 см.

Задача 3: Відстань від точки B до сторін ромба АВСD дорівнює 15 см, а до площини АВС – 9 см. Знайдіть радіус кола, вписаного в ромб.

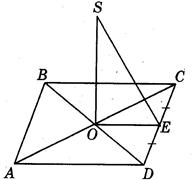
Дано:  АВСD – ромб; SО = 9 см, SE = 15 см

Знайти: ОE

Розв’язання:

ОЕ – радіус вписаного кола;

За т. Піфагора: ОЕ² = SE² – SО²

ОЕ²=15² – 9² = (15 – 9)(15 + 9) = 144

ОЕ = 12 см

Отже, ОЕ = 12 см

Задача 4: З вершини D прямокутника АВСD проведено перпендикуляр SD до його площини. АD=5 см, DC=16 см,

SD = 12 см. Знайти відстані від точки S до AD і CD.

Розв’язання:

SА і SС – шукані відстані(за т. про три перпендикуляра);

ADS та СDS-прямокутні (за озн. перпендикуляра):

За теоремою Піфагора:

SА²=SD²+АD² = 12²+5²

АS = 13 см

SС²=DS²+DС² = 12² + 16²

СS = 20 см

Отже, SА = 13 см; SС = 20 см

Задача 5: Дано куб  ABCDA₁B₁C₁D₁

Знайти: кут між прямими:

1) BC та СC₁

2) AC та ВС

3) ВС та C₁D₁

4) A₁B₁ та АС

Розв’язання:

1) прямі BC та СC₁ перпендикулярні, тому кут між ними дорівнює 90°;

2) пряма АС є діагоналлю основи куба і ділить кути А і С навпіл. Тому кут між прямими AC та ВС дорівнює 45°;

3) кут між мимобіжними прямими ВС та C₁D₁ дорівнює 90°;

4) кут між мимобіжними прямими A₁B₁ та АС  дорівнює 45°.

Тести

1. Виконайте тести за посиланням: https://vseosvita.ua/test/start/dcr965

2. Виконайте інтерактивну вправу:

Підготовка до НМТ з математики

1. Виконайте завдання за посиланням:  https://zno.osvita.ua/mathematics/tag-pryami_ta_ploshini_u_prostori/

Відео

Перегляньте навчальне відео:

Завдання для самостійної роботи

Математичний диктант

Дано зображення куба.

Користуючись цим зображенням, запишіть:

1)  площину, яка проходить через точку В прямої AВ і перпендику­лярна до неї;

2)  пряму, яка перпендикулярна до площини АВС і проходить через точку D;

3)  пряму, яка перпендикулярна до площини АВС і проходить через точку  ;

4)  площину, яка перпендикулярна до прямої BD;

5)  прямі, які перпендикулярні до площини АВС;

6)  площини, які перпендикулярні до прямої DC.