Зміст

1. Теоретичні відомості………………………………………..3 – 12

2. Приклади розв’язування типових завдань……..13 – 18

3. Тести, вебквест з теми………………………………………19

4. Підготовка до НМТ…………………………………………….20

5. Відео…………………………………………………………………..21 – 24

6. Завдання для самостійної роботи…………………….25 – 26

Теоретичні відомості

У повсякденному житті нам часто доводиться спостерігати процеси, у яких зміна однієї величини (незалежної змінної) призводить до зміни іншої величини (залежної змінної). Вивчення цих процесів потребує створення їх математичних моделей. Однією з таких найважливіших моделей є функція.

Функція — це така залежність, при якій кожному значенню х з деякої множини відповідає єдине значення змінної у. Записують це: y=f(x).

Змінну х– називають незалежною змінною, або аргументом.

Змінну у– називають залежною змінною, або функцією.

Усі значення, яких набуває незалежна змінна х називають областю визначення функції. Позначають буквою D.

Усі значення, яких набуває залежна змінна у називають областю значення функції або множиною значень функції та позначають буквою Е.

Способи задання функції

1. Аналітичний спосіб

Функція задається за допомогою формули.

2. Табличний спосіб

Цей метод полягає у тому, що відповідність між множиною значень змінної x і функції y задається у вигляді таблиці.

3. Графічний спосіб

Функція задається за допомогою графіка функції.

4. Словесний (описовий) спосіб

Словесний спосіб задання функції полягає в тому, що закон, за яким залежно від х обчислюється значення у, виражається словами. Цей спосіб використовується під час розв‘язування задач, в яких розглядаються взаємопов‘язані величини.

Що називають графіком функції

Графіком функції називається множина всіх точок  координатної площини, абсциси яких дорівнюють значенню аргумента, а ордината –значенню функції.

Види функцій, які ви вже знаєте

1. Лінійна функція 

Задається формулою: у = kх + b

Графіком лінійної функції є пряма.                     

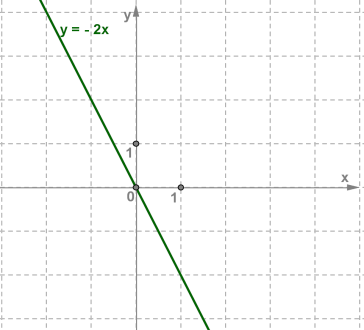
2. Пряма пропорційність

Задається формулою: у = kх

Графіком такої функції є пряма, яка проходить через       

початок координат.

3. Обернена пропорційність

Задається формулою: у = k/х

Графіком такої функції є гіпербола.

4. Функція у = х²

Графіком функції є парабола.

Парність та непарність функції

1. Функцію y=f(x), називають парною, якщо для будь-якого значення x з області визначення виконується рівність

f(−x) = f(x).

Графік будь-якої парної функції симетричний відносно осі у.

2.Функцію y=f(x),  називають непарною, якщо для будь-якого значення x з області визначення виконується рівність   f(−x) = − f(x).

Графік будь-якої непарної функції симетричний відносно початку координат.

Монотонність функції

1.Значення аргументу, при якому значення функції дорівнює 0, називають нулем функції.

2.Функцію у=f(x) називають зростаючою на проміжку X, якщо з нерівності x₁ > x₂, де x₁ і x₂ — будь-які дві точки проміжку X, випливає нерівність f(x₁) > f(x₂).

Функція зростає, якщо більшому значенню аргументу відповідає більше значення функції.

3.Функцію у=f(x) називають спадною на проміжку X, якщо з нерівності x₁ > x₂, де x₁ і x₂ — будь-які дві точки проміжку X, випливає нерівність f(x₁) < f(x₂).

Функція спадає, якщо більшому значенню аргументу відповідає менше значення функції.

4.Проміжки, на яких функція зберігає свій знак, називаються проміжками знакосталості функції.

Приклади розв’язування типових завдань

Задача 1

Знайти область визначення функції:

у = х – 1/х + 2

Розв’язання:

Оскільки знаменник дробу не може дорівнювати нулю, то областю визначення функції є множина усіх значень х, для яких х +2≠0, тобто х ≠ -2. Отже, D(y) = (-∞;-2) U (-2; +∞).

Задача 2

Знайти область значень функції:

у = -6/х

Розв’язання:

Областю значень будуть всі дійсні числа крім у = 0.

Отже, Е(y) = (-∞;0) U (0; +∞)

Задача 3

Дослідити на парність функцію:

f(x) = x² + 5

Розв’язання:

f(- x) = (- x)² + 5 = x² + 5

Отже, f(- x) = f(x).

Функція парна.

Задача 4

Дослідити на парність функцію:

f(x) = 8/х

Розв’язання:

f(- x) = 8/(-х) = – 8/х

Отже, f(- x) = – f(x)

Функція непарна.

Задача 5

Знайдіть нулі функції, проміжки зростання та спадання функції, зображеної на малюнку

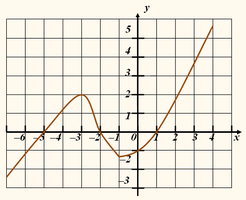
Розв’язання:

х₁ = -5; х₂ = -2; х₃ = 1 – нулі функції;

(-∞;-3) U (-1; +∞) – зростає;

(-3;-1) – спадає.

Задача 6

Знайдіть нулі функції: 1)у = 2х² – х – 6; 

                                   2) у = х²  – 36

Розв’язання:

1) у = 0

2х² – х – 6 = 0

D = 1 – 4 · 2 · 6 = 49

х₁ = 2; х₂ = – 1,5

Отже, х₁= – 1,5; х₂ = 2.

2) у = 0

х²  – 36 = 0

(х – 6)(х + 6) = 0

х – 6 = 0 або х + 6 = 0

х₁ = 6          х₂ = – 6

Отже, х₁= – 6; х₂ = 6.

Задача 7

Вкажіть проміжки знакосталості функції.

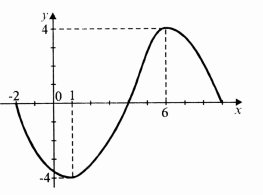
Розв’язання:

1) у > 0 при х є (4;9);

2) у < 0 при х є ( -2;4).

Тести, вебквест

1.Виконайте тести за  посиланням:

https://vseosvita.ua/test/start/ozo070

2. Пройдіть вебквест за посиланням:

https://vseosvita.ua/webquest/start/s/17968/319583-f8f386d6

3. Виконайте інтерактивну вправу:

Підготовка до НМТ з математики

1.Перегляньте відео за посиланням:

https://youtu.be/sgi8h9rRzBQ

2.Виконайте тести за посиланням:

https://zno.osvita.ua/mathematics/tag-funkcionalna_zalezhnist_vlastivosti/

Відео

Перегляньте відео за посиланням:

https://youtu.be/IpyRn63QfmY

Завдання для

самостійної роботи

1.Функцію задано формулою у = 2х – 1. Знайти значення функції, якщо значення аргументу дорівнює – 2.

2.Знайти значення аргументу, при якому функція у = 3х + 1 набуває значення  –8.

3.Знайти область визначення функції:   у = 5/(х – 2).

4.Не виконуючи побудови графіка, знайти нулі функції:

у = 3х – 12.

5.Яка з точок належить графіку функції:   у = 7х – 2?

а) (0; 4); б) (-2; – 12); в) (1; 5);  г) (- 1; – 7).

6.Графік функції y = −3x + b проходить через

точку з координатами (2;8). Знайдіть b.

7.Виразіть із формули 2x − 4y = 6 змінну х.