Періодичність, властивості та графіки тригонометричних функцій

Довідкові матеріали

Якщо при повороті навколо точки О на кут початковий радіус ОА переходить у радіус ОВ, то при повороті на кут  початковий радіус ОА перейде у радіус , симетричний ОВ відносно осі абсцис (рис.1).

Абсциси точок В і  рівні, а ординати рівні за модулем, але протилежні за знаком. Це означає, що , , , . Таким чином, функції , ,  непарні, а функція  парна.

Для періодичної функції  виконується рівність , де Т – відмінне від нуля число, назване періодом функції. Кожна періодична функція має велику кількість періодів, тобто якщо Т – період, то пТ – період, де , . Звичайно, говорячи про період, мають на увазі найменший додатний період, який називається основним. Основними періодами для тригонометричних функцій є:  для функцій , ;  для функцій , . У більш загальному вигляді можемо записати: , , , , .

Якщо кути виражаються в радіанах, то  – основний період функцій , ;  – основний період функцій , .

Відомо, що періоди функцій  і  обчислюються за формулою 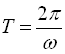, а періоди функцій  і  – за формулою .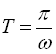

Якщо період функції  дорівнює , а період функції  дорівнює , то період функції  і  дорівнює найменшому числу, при діленні якого на  і  дістаємо цілі числа.