Зміст

1. Квадратні рівняння

2. Формула коренів квадратного рівняння

3. Теорема Вієта

4. Квадратний тричлен

5. Розв’язування рівнянь

6. Раціональні рівняння

Історія

Розв’язування рівнянь другого степеня, зокрема й квадратних, у стародавні часи було викликане потребою вирішувати проблеми пов’язані з поділом землі, знаходженням її площі, земельними роботами військового характеру, а також із розвитком таких наук, як математика й астрономія. Квадратні рівняння вміли розв’язувати вавилоняни близько 2000 років до н. е. Відомо, що їхні методи розв’язання майже збігаються із сучасними, проте невідомо, яким чином вавилоняни дійшли до цих методів: майже на всіх знайдених до того часу клинописних текстах збереглися лише вказівки щодо знаходження коренів рівнянь, але не зазначено, як вони були виведені. Однак, незважаючи на розвинутість математики у ті часи, в цих текстах немає згадки про від’ємні числа і про загальні методи розв’язування рівнянь. У стародавній Греції квадратні рівняння розв’язувалися за допомогою геометричних побудов. Правило знаходження коренів рівняння, зведеного до вигляду сучасного нам звичного вигляду уперше дав індійський вчений Брахмагупта. Аль-Хорезмі описав алгоритм знаходження коренів всіх шести підвидів квадратного рівняння. Він же й вивів формули залежності коренів рівняння від коефіцієнтів у 1591 році. Після праць нідерландського математика А. Жирара (1595 — 1632), а також Декарта і Ньютона спосіб розв’язування квадратних рівнянь набув сучасного вигляду.

Квадратним або рівнянням другого степеня з однією змінною називають рівняння виду ax²+bx+c=0, де x – змінна, а a,b,c – коефіцієнти квадратного рівняння, причому a≠0 .
Якщо коефіцієнт b або c дорівнює нулю, то квадратне рівняння називають неповним (неповне квадратне рівняння – pure quadratic). Неповні квадратні рівняння бувають трьох видів:
1) ax²=0;
2) ax²=bx=0;
3) ax²+c=0.

Рівняння ax²=0 має один корінь x=0.
Рівняння виду ax²=bx=0 рівносильне рівнянню x(ax+b)=0 і завжди має два корені: x=0 i x=-b/a.
Квадратне рівняння виду ax²+c=0 рівносильне рівнянню x²=-c/a.

Якщо -c/a>0, воно має два розв’язки

, якщо -c/a<0 – рівняння не має жодного розв’язку.

Приклад 1
Знайти корені рівняння 2x²-18=0.
Розв’язання
2x²-18=0;
2x²=18;
x²=9;

x12=±

x₁=3, x₂=-3;
Відповідь: x₁=3, x₂=-3.

Дискримінантом (дискримінант – discriminant) рівняння ax²+bx+c=0 називають вираз D=b²-4ac.
Якщо D>0 рівняння ax²+bx+c=0 має два розв’язки, які знаходяться за формулами

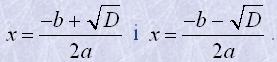
Якщо D=0 рівняння ax²+bx+c=0 має один розв’язок, який знаходиться за формулою

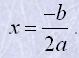
Якщо D<0 рівняння ax²+bx+c=0 не має жодного розв’язку.

Приклад 2
Знайти корені рівняння x²+4x-21=0.
Розв’язання
D=4²-4·1·(-21)=16+84=100>0.

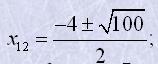
x₁=3, x₂=-7.
Відповідь: x₁=3, x₂=-7.

Квадратне рівняння називають зведеним (зведене квадратне рів-няння – reduced quadratic), якщо коефіцієнт a дорівнює одиниці: x²+px+q=0.

Якщо зведене квадратне рівняння x²+px+q=0 має два корені, то їх сума дорівнює коефіцієнту p рівняння, взятому з протилежним знаком, а добуток – вільному члену q:
x₁+x₂=-p;
x₁x₂=q,
де x₁,x₂ – розв’язки рівняння x²+px+q=0.

Дякую за увагу!